Zadání XXXI. ročníku

Protože je deltoidu opsaná kružnice, jedná se o tětivový čtyřúhelník, pro který platí, že součet jeho protilehlých úhlů je \(180°\). Ze zadání víme, že se velikosti úhlů \(\angle ABC\) a \(\angle CDA\) rovnají, proto platí, že \(|\angle ABC|=|\angle CDA|=90°\).

Podíváme se na krajní situace:

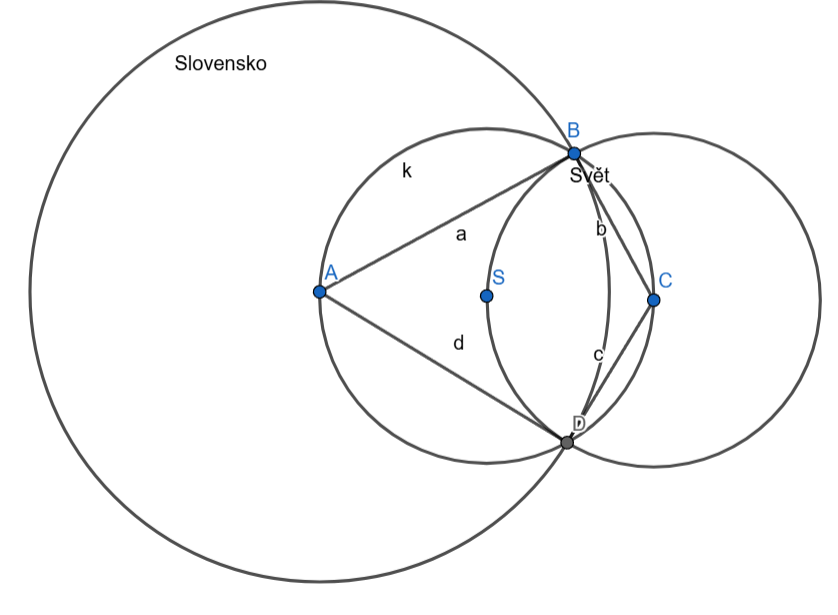
Pokud by kružnice \(Svět\) procházela bodem \(S\), pak budou trojúhelníky \(\triangle BCS\) a \(\triangle DCS\) rovnostranné. (Kružnice \(Svět\) i kružnice \(k\) jsou stejně velké, protože sdílí poloměr \(|SC|\) a zároveň \(|DC|\) i \(|BC|\) jsou poloměry kružnice \(Svět\), proto \(|SC|=|DC|=|BC|\).) Úhel \(\angle BCD\) má tedy \(120°\) (2x60°), takže \(|\angle BAD|\) je \(60°\) (součet protilehlých úhlů v tětivovém čtyřúhelníku je \(180°\)). Aby bod \(S\) ležel uvnitř kruhu \(Svět\), musí být velikost úhlu \(\angle BAD\) větší nebo rovna \(60°\).

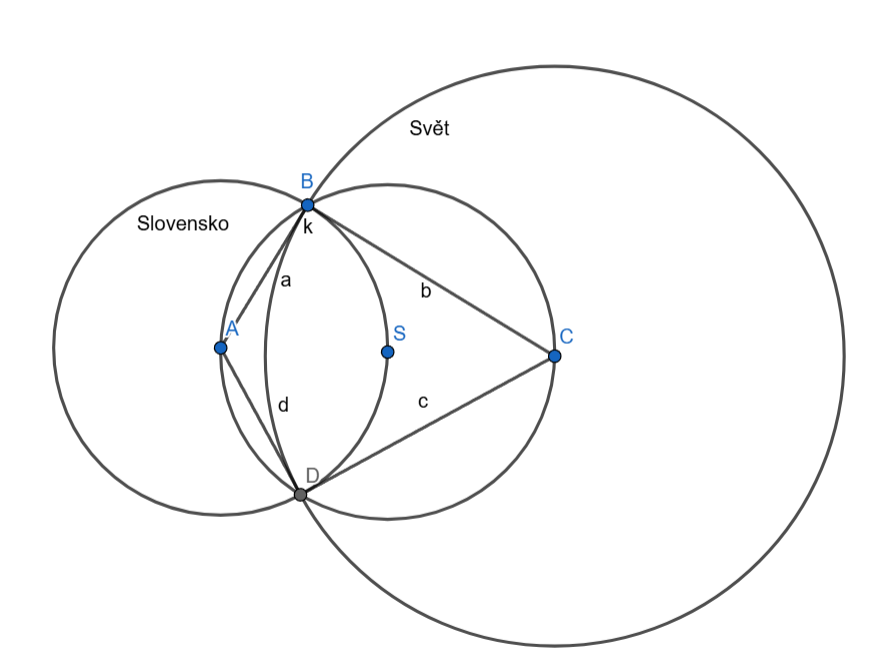
Pokud by kružnice \(Slovensko\) procházela bodem \(S\), pak budou trojúhelníky \(\triangle BAS\) a \(\triangle DAS\) rovnostranné. (Kružnice \(Slovensko\) i kružnice \(k\) jsou stejně velké, protože sdílí poloměr \(|SA|\) a zároveň \(|DA|\) i \(|BA|\) jsou poloměry kružnice \(Slovensko\), proto \(|SA|=|DA|=|BA|\).) Úhel \(\angle BAD\) má tedy \(12°\) (2x60°). Aby bod \(S\) ležel uvnitř kruhu \(Slovensko\), musí být velikost úhlu \(\angle BAD\) menší nebo rovna \(120°\).

Takže aby bod \(S\) ležel v průniku kruhů určenými kružnicemi \(Svět\) a \(Slovensko\), musí \(|BAD|\) náležet do uzavřeného intervalu \(<60°,120°>\).

Průnik dvou kružnic může být buď jeden, dva, nebo nekonečně mnoho (pokud jsou kružnice totožné). Kružnice \(Svět\) a \(Slovensko\) totožné nejsou, protože mají dva různé středy. Proto je maximální počet průsečíků těchto dvou kružnic 2. Těmi jsou ale už body \(B\) a \(D\), proto bod \(S\) už dalším průsečíkem není, pokud některé z těchto tří bodů nesplývají. Body \(B\) a \(D\) jsou určitě různé, protože to jsou dva různé vrcholy čtyřúhelníku a \(S\) je různý od \(B\) i \(D\), protože \(B\) a \(D\) leží na obvodu kružnice \(k\) a \(S\) je její střed.

K řešení jste se dostali různými způsoby, nejčastěji jste posouvali bodem B (případně bodem D) a zkoumali jste, jak se mění poloha kružnic a kruhů vůči středu S. Někteří jste posouvali průsečíkem úhlopříček deltoidu. Objevilo se i jedno řešení pomocí goniometrických funkcí. V podstatě všichni jste nakonec došli ke správným výsledkům a nejčastějím problémem bylo asi to, že někteří u 1. nespecifikovali, jestli se jedná o otevřený, nebo uzavřený interval.

Uvažujme kružnici opsanou trojúhelníku \(ACE\). Kružnice procházející všemi třemi body je jen jedna a to \(k\). Tedy na kružnici opsané trojúhelníku \(ACE\) leží i body \(B,D,F\). Protože \(|AB| = |BC|\), musí bod \(B\) ležet na ose strany \(AC\). Tedy \(B\) je Švrčkovým bodem trojúhelníku \(ACE\) naproti bodu \(E\). Pak přímka \(EB\) je osou úhlu \(\angle AEC\). Podobně přímky \(AD, CF\) jsou po řadě osami úhlů \(\angle EAC, \angle ACE\). Tedy zadané úsečky jsou osami úhlů v trojúhelníku a ty se vždy protínají v jednom bodě.

Odevzdaná řešení byla hezká, chválím všechny. Potěšilo mě že někteří dokázali i v této úloze přijít s originálními způsoby řešení. Naopak se neopakovaly žádné výrazné chyby. Jen tak dál!

Označme si body dotyku kružnic se stranami čtyřúhelníka:
\(K\) - strana \(AB\), kružnice \(k_1\)
\(L\) - strana \(BC\), kružnice \(k_2\)
\(M\) - strana \(CD\), kružnice \(k_2\)
\(N\) - strana \(AD\), kružnice \(k_3\)
Dále z mocnosti bodu ke kružnici víme, že
\(|AK|=|AN|\)
\(|BK|=|BX|\)
\(|DX|=|DN|\)
\(|CL|=|CM|\)
\(|BL|=|BY|\)
\(|DY|=|DM|\)
Pro tečnový čtyřúhelník platí:
\(|AB| + |CD| = |BC| + |DA|\)
což můžeme pomocí výše vypsaných rovnic přepsat jako:
\((|AK|+|KB|)+(|CM|+|MD|)=(|BL|+|LC|)+(|DN|+|NA|)\) (body dotyku leží na straně, proto si délky odpovídají)
\(|AN|+|BX|+|CL|+|DY|=|BY|+|LC|+|DX|+|NA|\) $~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ $ \(-|AN|-|CL|\)
\(|BX|+|DY|=|BY|+|DX|\) $~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ $ \(|BX|=|BD|-|DX|\); \(|BY|=|BD|-|DY|\)
\(|BD|-|DX|+|DY|=|BD|-|DY|+|DX|\)
\(2|DY|=2|DX|\) \(=>\) \(|DY|=|DX|\)
Víme, že bod \(X\) i bod \(Y\) leží na úsečce \(BD\), proto \(X=Y\)

Většina z vás si s úlohou poradila opravdu dobře! Spousta potřebných informací byla přímo ve studijním textu, takže jsem byla při hodnocení mírná a ani jsem nepožadovala podrobné důkazy.

Uvědomme si, že každé dvě kružnice budou mít dva průsečíky - jedním budou příslušné středy stran. Ten druhý musí existovat, protože kdyby se dotýkaly jen v jednom bodě, nacházeli bychom se v případě pravoúhlého trojúhelníka, ze zadání ale máme, že \(ABC\) je ostroúhlý.

Všimneme si, že všechny tři kružnice opsané menším trojúhelníkům se protínají ve středu kružnice opsané trojúhelníku \(ABC\). Musíme to ale ukázat. \(AS_cS_b\) je trojúhelník podobný trojúhelníku ABC, oba jsou dokonce stejnolehlé, se středem v bodě \(A\) a koeficientem \(\frac{1}{2}\), v této stejnolehlosti se na sebe musí zobrazit i středy kružnic opsaných malému a velkému trojúhelníku. Budou tedy ležet na jedné přímce i s bodem A, přičemž \(2|AO_a| = |AO|\), kde \(O_a\) je střed kružnice opsané \(AS_bS_c\) a \(O\) je střed kružnice opsané \(ABC\), tím pádem bod O spadne na kružnici opsanou \(AS_bS_c\), analogicky ukážeme, že se bude nacházet i na kružnicích opsaným zbylým menším trojúhelníkům.

Uvědomme si ještě, že středy stran \(S_a, S_b, S_c\) leží na Feurbachově kružnici. Ze studijního textu pak víme, že střed Feuerbachovy kružnice, těžiště \(ABC\) a střed kružnice opsané \(O\) leží na Eulerově přímce. Tím jsme hotovi.

Došlá řešení byla správná! Chválím využítí stejnolehlosti při dokazování, že střed \(O\) leží na kružnici. Nacházela se i jiná řešení - někteří to ukazovali přes osy stran, někteří zase ukazovali, že se kružnice protínají v ortocentru trojúhelníka \(S_aS_bS_c\), což je mimochodem shodný bod se středem kružnice opsané trojúhelníku \(ABC\). Dobrá práce!

Zaměříme se na šestiúhelníky tvořené právě třemi políčky. V každém takovémto šestiúhelníku spolu sousedí všechna políčka. Pokud rozdíl každých dvou nemá být dělitelný třemi, musí čísla vepsaná do políček dávat zbytky \(0, 1\) a \(2\) (mod \(3\)). Kdyby nějaká dvě políčka dávala stejný zbytek \(r\), dala by se zapsat jako \(3a+r\) a \(3b+r\) a jejich rozdíl by byl \(3a+r-3b-r=3(a-b)\), což je zřejmě dělitelné třemi.

Pojďme se tedy podívat na to, jaké součty nám tyto šestiúhelníky mohou dát. Pokud máme splněnou první podmínku, tak si čísla v jednom šestiúhelníku můžeme zapsat jako \(3a\), \(3b+1\) c \(3c+2\). Když je nyní sečteme, dostáváme \(3a+3b+1+3c+2=3(a+b+c+1)\). Všechny součty tedy budou dělitelné třemi a nejmenší možný je \(3\) a největší je \(27\) (\(0\) ani \(30\) při splnění první podmínky dostat nemůžeme). Celkem tedy můžeme dostat \(9\) různých součtů (konkrétně \(3,6,9,12,15,18,21,24\) a \(27\)), ale šestiúhelníků je \(10\). Vždy budou tedy existovat minimálně \(2\) šestiúhelníky, které budou dávat stejný součet a nelze tabulku vyplnit tak, aby byly splněny obě podmínky zároveň.

Všichni jste to měli naprosto správně. Skvělá práce!

Když si vypíšeme prvních několik členů obou posloupností, můžeme si všimnout, že by vzorec pro \(P_n\) mohl být takový, že pro sudá \(n\) platí \(P_n=0\) a pro lichá \(n\) platí \(P_n=-F_{n+1}\). Domněnku dokážeme matematickou indukcí.

Báze: Pro \(n=0\) platí \(P_0=0\) a pro \(n=1\) platí \(P_1=-1=-F_2\).

Indukční předpoklad: Mějme libovolné \(n \geq 2\). Předpokládejme nyní, že pro všechna \(m<n\) platí \(P_m = 0\) pro \(m\) sudé a \(P_m = -F_{m+1}\) pro \(m\) liché.

Indukční krok: Samotný indukční krok rozdělíme na dva příklady.

Nechť je \(n\) sudé, tedy \(n=2k\) pro nějaké \(k \in \mathbb{N}\). Pak \[P_n = P_{2k} = P_{2k-1} + P_{2k-2} + (-1)^{2k} \cdot F_{2k} = -F_{2k-1+1} + F_{2k} = 0\]

Nechť je \(n\) liché, tedy \(n=2k+1\) pro nějaké \(k \in \mathbb{N}\). Pak \[P_n = P_{2k+1} = P_{2k} + P_{2k-1} + (-1)^{2k+1} \cdot F_{2k+1} = -F_{2k-1+1} - F_{2k+1} = -F_{2k+2} = -F_{n+1}\]

Tím jsme dokázali předpoklad, že \(P_n\) se dá vyjádřit jako \(P_n=0\) pro sudá \(n\) a \(P_n=-F_{n+1}\) pro lichá \(n\).

Kdyby po nás zadání chtělo explicitní vyjádření bez použití funkce \(F_n\), můžeme si \(F_n\) vyjádřit jako \[F_n = - \frac{\phi^{n}}{\sqrt{5}} + \frac{(1-\phi)^{n}}{\sqrt{5}}.\]

Obecně se vám tato úloha dařila. Většina z vás své řešení dokazovala matematickou indukcí podobně jako vzorové řešení. Mám jen pár obecných rad: * Když dokazujete indukcí a používáte indukční předpoklad, nekde explicitně uveďte co považujete za předpoklad (+ jeslti platí pro předchozí n, případně pro všechna menší apod.). * Čtěte si po sobě svá řešení, ať vám v nich nezůstávají znaménkové nebo češtinářské chyby.

Jinak super, hodně zdaru i nadále :) Terka Ki.

Rovnice po řadě označme \((1), (2), (3), (4)\). Můžeme si všimnout, že sečtením \((1) + (4)\) a \((2) + (3)\) dostaneme v obou případech na pravé straně \(5a\). Můžeme tedy porovnat levé strany a výraz zjednodušit:

\[x^2 + y^2 + z^2 + w^2 + zw + xy = x^2 + y^2 + z^2 + w^2 + xw + yz\] \[zw + xy - xw - yz\] \[z(w-y) - x(w-y) = 0\] \[(z-x)(w-y) = 0.\]

Nutná podmínka pro platnost soustavy je tedy (nezávisle na hodnotě \(a\)) \(x=z \vee y=w\). Můžeme si všimnout, že při \(x = z\) jsou levé strany rovnic \((1)\) a \((2)\) totožné, což implikuje \(a = 2a\) a tedy \(a = 0\). Obdobně při \(y = w\) jsou totožné levé strany rovnic \((1)\) a \((3)\), tedy \(a = 3a\), z čehož opět \(a = 0\). Z podmínky tak přímo vyplývá, že pokud má soustava řešení, pak \(a = 0\). Obměnou nenulovost \(a\) implikuje, že neexistuje žádné řešení soustavy.

Pojďme nyní všechna řešení pro \(a = 0\) nalézt. Sečtením všech čtyř rovnic (pro \(a = 0\)) a následnou úpravou na čtverce dostáváme:

\[2(x^2 + y^2 + z^2 + w^2) + zw + xw + yz + xy = 0\] \[\frac{(x+y)^2+(y+z)^2+(z+w)^2+(x+w)^2}{2} + x^2+y^2+z^2+w^2 = 0,\]

z čehož okamžitě vidíme, že \(x = y = z = w = 0\) je jediné řešení soustavy pro \(a = 0\), jelikož levá strana rovnice obsahuje pouze nezáporná čísla (druhé mocniny reálných čísel jsou vždy nezáporné).

Celkem tedy vidíme, že pro \(a \neq 0\) neexistuje řešení v \(\mathbb{R}\) a pro \(a = 0\) má soustava řešení pouze pro \(x = y = z = w = 0\) v tomto oboru.

Úloha měla hodně dobrou úspěšnost. Občasné chyby byly z přehlédnutí, ztracené nulové řešení po dělení proměnnou, případně nedostatečné dokázání, že existuje právě jedno řešení. Celkově ale moc fajn :)

Nejprve ukážeme, že počet přímých cest mezi městy nepřekročí \(n+m-1\). V obou státech dohromady je \(n+m\) měst; představme si, že mezi žádnými dvěma nevede cesta, a města tedy tvoří \(m+n\) navzájem nepropojených komponent. Když nyní přidáme cestu spojující dvě města, propojíme navzájem dvě komponenty a počet nepropojených komponent se o jedna sníží. Zároveň platí, že mezi dvěma městy existuje cesta (ne nutně přímá), právě když jsou součástí jedné komponenty. Pokud bychom přidali přímou cestu mezi městy, která už jsou součástí jedné komponenty, existovaly by mezi nimi nejméně dvě různé cesty a jejich spojením by vznikla kružnice. Jediné cesty, které tedy můžeme mezi města přidávat, jsou ty, které počet komponent snižují o \(1\). Je zřejmé, že na konci musí existovat alespoň jedna komponenta, a tak můžeme mezi \(n+m\) měst přidat nejvýše \(n+m-1\) cest.

Abychom ukázali, že takového \(k\) lze dosáhnout, najdeme pro každou dvojici \(n, m\) konstrukci obsahující \(n+m-1\) přímých cest. Vybereme si v každém státě jedno hlavní město; tomu na Slovensku budeme říkat Bratislava a tomu ve Světě Brno. Jako první propojíme Bratislavu se všemi městy ve Světě, tím vznikne \(n\) přímých cest. Dále Brno propojíme se všemi městy na Slovensku kromě Bratislavy, protože mezi nimi cesta už existuje. Tím sestrojíme dalších \(m-1\) přímých cest, dohromady jich tedy máme \(n+m-1\).

Všechna města kromě Brna a Bratislavy jsou v naší konstrukci propojena pouze s jedním dalším městem, a tak nemohou být součástí kružnice (jakmile do nich dojedeme, můžeme pokračovat pouze toutéž cestou, kterou jsme do nich přijeli). Jediná města, která by tedy mohla tvořit kružnici, jsou Brno a Bratislava, kružnice mezi pouze dvěma městy ale vzniknout nemůže, a tak naše konstrukce odpovídá zadání a ukázali jsme, že \(k=n+m-1\).

Většina řešení využívala teorie grafů a rychle přišla na správnou odpověď. Je důležité potom nezapomenout také ukázat, že daná konstrukce opravdu existuje a splňuje zadání. Párkrát jsem strhávala body kvůli nedostatečnému a chaotickému komentáři řešení – zejména u těchto „obkecávacích" důkazů je potřeba dbát na to, aby na sebe myšlenky navazovaly a neskákali jste od jedné ke druhé.