Zadání XXXII. ročníku
3. série
Posloupnosti
Termín odevzdání: 5. ledna 2026 23:59
Finťa byla u krále „na návštěvě“. Stráže ji doprovodili do přepychového pokoje, což Finťa poznala podle toho, že na podlaze ležel tygrovaný koberec, zdi lemovaly nevkusně groteskní obrazy a nábytek byl ozdobený různobarevnými saténovými potahy. Lidé se k ní chovali na oko slušně, nicméně bylo zřejmé, že je v tomto domě vězněm.
Za dveřmi slyšela dohadovat se hlasy, bohužel ale nebyla schopná od sebe rozeznat jednotlivá slova. Potom, co hlasy utichly, se otevřely dveře a do nich vrazil král Čtvrtý. Pokynul Fintě, aby se posadila na židli a sám se posadil na opačný konec skoro nekonečně dlouhého stolu. Pokynul všem sloužícím, aby opustili místnost. Neviditelné ruce stiskly Fintě žaludek, co se bude dít?
Úloha 1 – Další šáhlý Tribonacci:
Mějme rekurentně definovanou posloupnost \[T_0=0, T_1=1, T_2=-1\] \[T_n= T_{n-2} -T_{n-3}\] Dokažte, že se v posloupnosti vyskytuje pouze konečně mnoho nul.
Řešení
Vypíšeme si prvních pár členů posloupnosti: \[T_0=0, T_1=1, T_2=-1, T_3=1, T_4=-2, T_5=2 \dots\] Vidíme, že při výpočtu dalších a dalších členů posloupnosti nastane vždy jeden ze dvou případů: buď od kladného čísla odečítáme záporné, nebo od záporného čísla odečítáme kladné. Nabízí se tedy tvrzení, které už jednoduše dokážeme indukcí.
Tvrzení: Pro \(n\in\N\) je \(T_{2n-1}>0\) a \(T_{2n}<0\).
Důkaz:
Bázový krok n=1: \(T_1=1>0, T_2=-1<0\)
Předpokládejme, že tvrzení bylo dokázáno pro všechna \(n \in \{1,2,\dots,k\}\) a my ho nyní chceme dokázat pro \(n=k+1\).
\(T_{2(k+1)-1}=T_{2k+1}=T_{2k-1}-T_{2(k-1)}\) Z předpokladů ale víme, že \(T_{2k-1}>0\) a \(T_{2(k-1)}<0\). Celkem tedy dostáváme \(T_{2(k+1)-1}=T_{2k-1}-T_{2(k-1)}>0\).
\(T_{2(k+1)}=T_{2k+2}=T_{2k}-T_{2k-1}\) Z předpokladů ale opět už víme, že \(T_{2k}<0\) a \(T_{2k-1}>0\). Celkem tedy máme \(T_{2(k+1)}=T_{2k}-T_{2k-1}<0\), čímž je tvrzení dokázáno.
Od indexu \(1\) budou členy posloupnosti tedy vždy buď kladné (pro liché indexy), nebo záporné (pro sudé), nikoli však nulové. Posloupnost tedy obsahuje konečný počet nul a to konkrétně jednu \(T_0=0\).
Komentář
Většina z vás měla úlohu naprosto správně.
Král Čtvrtý musel trochu křičet, aby ho vůbec Finťa slyšela přes tu bizarní vzdálenost. „Odkud jsi?“ Trochu mnohoznačná otázka. „Nejsem úplně odtud, jsem z Brkosovic. Chodím tam do školy.“ „Brkosovice, hm,“ zamyslel se král. V pobledlém světle vypadal ještě hůř než když byl ozářen reflektory na oslavách. Oči měl vypouklé a lemovaly je obrovské černé kruhy. Její hřeben měl víc vlasů než král a jeho barva se blížila omyvatelné Sekundalex barvě z kutilského obchodu BowHouse. „Brkosovicím nevládnu.“
„Nikdo nevládne Brkosovicím, pane, ani ředitel Říďa. Žijí si svým vlastní životem. Ale chtěla jsem spíš říct, že jsem z úplně jiného světa.“
„To jsou vipná ta vaše jména. Finťa, Říďa. Hehe, docela skibidi, co?“ ušklíbl se král.
Úloha 2 – Skibidi množina:
Množinu M přirozených čísel nazveme skibidi, jestliže každý její prvek kromě dvou lze jednoznačně vyjádřit jako součet jiných dvou prvků. Dokažte, že existuje nekonečně mnoho nekonečně velkých skibidi množin.
Řešení
Definujme posloupnost \(a_1=1\), \(a_2>1\in \mathbb{N}\), \(a_n=a_{n-1}+a_{n-2}\), pro \(n>2\). Ukážeme, že množina \(M\) prvků této posloupnosti je skibidi. Posloupnost je zřejmě rostoucí a každý člen přirozený. Proto existují nejmenší dva prvky množiny \(M\), jsou jimi právě \(a_1\), \(a_2\). Tyto nejdou zapsat ve tvaru součtu jiných prvků z množiny \(M\). Každý další lze vyjádřit ve tvaru součtu jako $a_n=a_{n-1}+a_{n-2}. Předpokládejme, že to lze i jiným způsobem. Buď by jeden ze sčítanců musel být větší nebo roven než \(a_{n}\), potom by i součet byl větší než \(a_n\). V opačném případě budou oba sčítance menší nebo rovny než \(a_{n-1}\), tudíž jejich součet bude menší než \(a_n\). Vyjádření součtu je tedy jednoznačné, proto je \(M\) skibidi.
Množina \(M\) je zjevně nekonečně velká.
Nekonečné množství těchto nekonečných skibidi množin zaručíme nekonečným množstvím možností pro volbu \(a_2\).
Komentář
Téměř všichni si s úlohou poradili, většina z vás pomocí Fibonacciho posloupnosti.
Fintě bylo na zvracení. Nadměrné používání gen-\(\alpha\) slangu v ní vyvolávalo the ICK, bez čepice, fr, fr.
„A co máš v plánu dělat v našem světě?“ zeptal se král.
„No chtěla jsem zajít na nějaké nákupy, podívat se po památkách, dát si nějaký dobrý jídlo,“ rozhazovala Finťa rukama, množství bylo nespočetně. „Taková basic turistka.“
„Teroristka?“ zhrozil se král.
„Turistka.“
„No ať to znamená cokoliv, myslím, že je na čase, aby ses takříkajíc vrátila, odkud jsi přišla.“
„Nemohla bych souhlasit víc.“
Úloha 3 – Zlomková rekurze:
Mějme rekurzivně definovanou posloupnost: \(a_{n+1}=\left(\frac{n!}{a_n}\right)^{(-1)^n}\) a víme, že \(a_{2025}=\frac{2025!}{a_1}\). Jakých všech hodnot může nabývat \(a_1\)? Výsledek nemusíte vyčíslit.
Řešení
Uvažujme \(a_n\) liché a vyjádřeme jeho pomocí další členy:
\(a_{n+1} = \frac{a_n}{n!}\),
\(a_{n+2} = \frac{(n+1)!}{a_{n+1}} = \frac{n!(n+1)!}{a_n}\),
\(a_{n+3} = \frac{a_{n+2}}{(n+2)!} = \frac{n!(n+1)!}{(n+2)!a_n}\),
\(a_{n+4} = \frac{(n+3)!}{a_{n+3}} = a_n\frac{(n+3)!(n+2)!}{n!(n+1)!}=a_n(n+1)(n+2)^2(n+3)\)
Vidíme, že lze poměrně elegantně vyjádřit \(a_{n+4k}\) pomocí \(a_n\). To se nám hodí, neboť 4(2025-1) a můžeme takto vyjádřit \(a_{2025}\) pomocí \(a_1\). Celkem máme dvě různá vyjádření pro vztah mezi \(a_1\) a \(a_{2025}\):
\(a_{2025}=\frac{2025!}{a_1}\) a \(a_{2025} = a_1 (2 \cdot 3^2 \cdot 4) (6 \cdot 7^2 \cdot 8) \cdots (2022 \cdot 2023^2 \cdot 2024)\), jejich spojením a úpravami dostáváme
\(a_1^2 = \frac{2025!}{(2 \cdot 3^2 \cdot 4) (6 \cdot 7^2 \cdot 8) \cdots (2022 \cdot 2023^2 \cdot 2024)} = \frac{5}{3} \frac{9}{7} \cdots \frac{2025}{2023} \Rightarrow a_1 = \pm \sqrt{\frac{5}{3} \frac{9}{7} \cdots \frac{2025}{2023}}\)
pozn. Uznávali jsme i řešení bez vykrácení faktoriálů - výsledek je pak tvaru \(a_1 = \pm \sqrt{\frac{2025! 2022! 2021! 2018! \cdots 2! 1!}{2024! 2023! 2020! \cdots 4! 3!}}\)
Komentář
Se samotnou úlohou nebyl větší problém. Překvapilo mě ale, že téměř polovina z vás nezvládla v posledním kroku správně odmocnit kladné racionální číslo! Doporučuji zopakovat…
„Výborně, pak tedy není nad čím diskutovat. Ty se vrátíš zpátky do svého světa a já tě nebudu muset odstranit jako toho předchozího.
“Toho předchozího? Fintě začala blikat kontrolka v hlavě. Něco bylo špatně.
„Vy se kvůli mně bojíte o svoji korunu?“
„Haha,“ utrousil král, ale jeho obočí se nad propadlýma očima skoro spojovala. „Já nemám proč se bát, lidé mě milují.“
„Proto máte všude kolem hradu tolik stráží?“ Občas Finťa neumí zavřít pusu. Teď přišel ten moment jejího života, kdy toho litovala. Odstranit přechozího? Byl to jeho předchůdce, král Třetí?
Jakýkoliv náznak úsměvu zmizel z králova obličeje. „Co si mě tu opovažuješ urážet, ty ubohá, neznámá, průměrná holko!“
Úloha 4 – Průměrná posloupnost:
Máme nekonstantní posloupnost \(A\) 2025 čísel. V prvním kroku vytvoříme novou posloupnost \(B\) tak, že jako i-tý člen vezmeme minimum i-tého člene předchozí posloupnosti a aritmetického průměru jeho dvou sousedních členů, tedy \(b_i = min\left\{a_i, \frac{(a_{i-1}+a_{i+1})}{2}\right\}\). (Bereme to tak, že první a poslední člen spolu sousedí.) V druhém kroku vytvoříme stejným způsobem posloupnost \(C\) z posloupnosti \(B\), pak \(D\) z \(C\) a tak dále. Řekneme, že posloupnost se ustálí, pokud už se v dalších krocích nemění. Po kolika krocích se může posloupnost ustálit?
Řešení
Nejdřív se podívejme, jak může vypadat ustálená posloupnost. Je zřejmé, že konstatní posloupnost je ustálená, a sporem dokážeme, že žádná jiná už ne. Připusťme, že máme posloupnost, která je ustálená, ale není konstatní. Potom v takové posloupnosti existuje maximální prvek (největší nebo jeden z největších) \(x_i\) takový, že \(x_{i+1}<x_i\). Jelikož je posloupnost ustálená, znamená to, že \[min\{x_i, \frac{x_{i-1} + x_{i+1}}{2}\} = x_i,\] tedy že \[x_i \leq \frac{x_{i-1} + x_{i+1}}{2}.\]
Spolu s \(x_{i+1}<x_i\) z toho vyplývá \(x_{i-1}>x_i\), což je ale spor s tím, že \(x_i\) je maximální prvek.
Nyní nám zbývá vyšetřit, po kolika krocích se z nekonstantní posloupnosti může stát konstantní. Určitě to může nastat po jednom kroku – třeba v posloupnosti, která obsahuje jednu jedničku a jinak samé nuly. Naopak existují posloupnosti, které se neustálí nikdy, stačí vzít posloupnost se dvěma sousedícími jedničkami a samými nulami jinde. Nenulové členy se v každém kroku zmenší na polovinu zprůměrováním s nulou a ke konstatní posloupnosti sice budeme konvergovat, ale v konečném počtu kroků jí nedosáhneme.
Mějme posloupnost a předpokládejme, že se po několika krocích ustálí. Označme \(y\) její minimální prvek. Proces tvoření nových posloupností je nerostoucí pro každý člen, proto minimální prvky budou vždy menší nebo rovny \(y\) a jistě nemůžeme dosáhnout menšího prvku než \(y\) průměrováním nějakých větších. Proto se posloupnost musí ustálit tak, že všechny prvky budou rovny \(y\).
Aby se člen různý od \(y\) změnil na \(y\), musí průměr jeho sousedů být \(y\). Jelikož jde o minimální prvek celé posloupnosti, musejí oba sousedé být rovni \(y\). Máme-li na začátku dva sousedící prvky, které jsou oba ostře větší než \(y\), nemohou nikdy na odpovídajících místech vzniknout \(y\). Došli jsme k tomu, že aby se posloupnost někdy ustálila, musí minimální prvek \(y\) být nejméně na každém druhém místě. Taková posloupnost se zřejmě ustálí v jediném kroku.
Závěrem tedy je, že pokud se posloupnost ustálí, je to vždy po právě jednom kroku.
Komentář
Moc se vás do úlohy nepustilo, ale téměř všichni, kteří jste řešení odevzdali, jste je měli naprosto správně. Super práce!
„Snažím se ti tu pomáhat, ty nevděčnice! Zavolám ti nejpovolanějšího člověka. Devěte!“Oh proboha jen to ne! pomyslela si Finťa. To už ale před ní stál, tentokrát alespoň zahalený, věštec.
„Je tvoje Devěte, neboj se jí to trochu okořenit,“ zašklebil se král a rázným krokem ji zanechal osamělou s podivínským věštcem.
Úloha A – Okořeněný polynom:
\(P(x)\) je polynom s celočíselnými koeficienty a konečným počtem členů. Platí pro něj \(xP(x+1)=(x+1)P(x+3)\). Najděte všechny vyhovující polynomy.
Řešení
Dosaďme \(x=0\): \[\begin{aligned} xP(x+1) &= (x+1)P(x+3)\\ 0 &= P(3)\end{aligned}\]
Z čehož vyplývá, že 3 je také kořen. Ukážeme, že lichá čísla větší než 2 jsou kořenem. Jak? Matematickou indukcí.
Bázový krok: Pro \(2k+1 =3\) je \(3\) kořenem.
Indukční krok: Předpokládejme, že pro všechna \(1, \dots k\) jsou \(3, 5, \dots 2k+1\) kořenem polynomu \(P(x)\). Pak dosaďme za \(x=2k\) \[\begin{aligned} 2kP(2k+1) &= (2k+1)P(2k+3)\\ 0 &= (2k+1)P(2k+3)\end{aligned}\]
Protože \(2k+1\) bylo kořenem polynomu tak je levá strana nulová. Protože navíc \(2k+1\) je kladné, dostáváme \(P(2k+3)=0\), tedy, že \(2k+3\) je kořenem. Polynom má kořen ve všech lichých číslech. Víme, že polynom \(n\)-tého stupňě má nejvýše \(n\) kořenů. Jediný polynom s nekonečně mnoha kořeny je polynom konstantně nulový.
Komentář
Většina řešení byla vesměs správná, super! Objevila se i řešení pomocí koeficientů polynomu, ta však byla argumentačně obtížnější.
Finťa ale už věděla, co se stane. Nebyla holkou první den. Bohužel se jí tohle stalo už několikrát. Snažila se vypadat dobře, starala se o sebe, nosila barevné outfity, ale nikdy to nedělala pro nikoho jiného, vždycky pro sebe. Ale oni to nechápali, mysleli si, že její sukně, její tričko, byla nějaká zpráva pro ně. Nikdy.
Měla toho dost. Byla blondýnkou studující matematiku. Nikdo ji nebral vážně, její úsměvy braly jako vyjádření její hlouposti a mysleli si, že růžové outfity znevažují její inteligenci.
Byl čas ukázat světu, že jejich předsudky jsou špatně.
Úloha B – Je čas:
Máme hodiny. Zaznačíme si body \(A_{12}\), \(A_2\), \(A_5\), \(A_8\), \(A_9\), kde index určuje pozici na ciferníku. Označme si bod \(B_1\) jako druhý průsečík kružnic nad úsečkami \(A_2A_{12}\), \(A_8A_{12}\) (jako první průsečík bereme společný bod úseček). \(B_2\) bude druhý průsečík kružnic nad \(A_2A_5\), \(A_5A_8\). \(B_3\) druhý průsečík kružnic nad \(A_8A_9\) a \(A_2A_9\). Ukažte, že \(B_1\), \(B_2\) a \(B_3\) leží na jedné přímce.
Pozn.: sestrojení kružnice nad úsečkou znamená, že střed kružnice bude ve středu úsečky a krajní body úsečky leží na dané kružnici (úsečka tvoří průměr kružnice)
Řešení
Máme náčrt našeho příkladu.
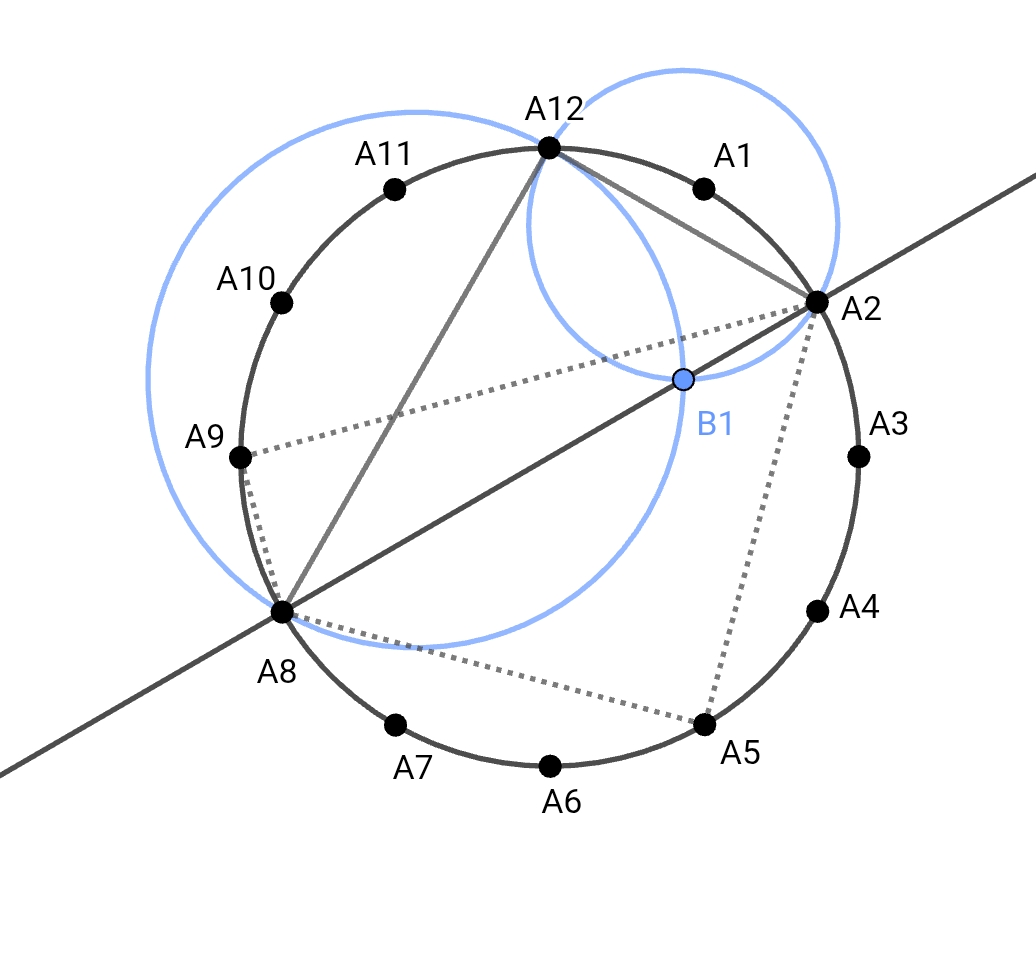
Díky pravidelnosti ciferníku víme, že úsečka \(A_2A_8\) je průměrem našeho ciferníku. Také si můžeme všimnout, že všechny zadané trojice bodů (\(A_2,A_{12},A_8; A_2,A_5,A_8; A_2,A_9,A_8\)) obsahují body \(A_2,A_8\). Thaletova věta nám říká, že trojúhelníky tvořené těmito trojicemi budou pravoúhlé a mají společnou přeponu \(A_2A_8\).
Nyní se podíváme na libovolný pravoúhlý trojúhelník.
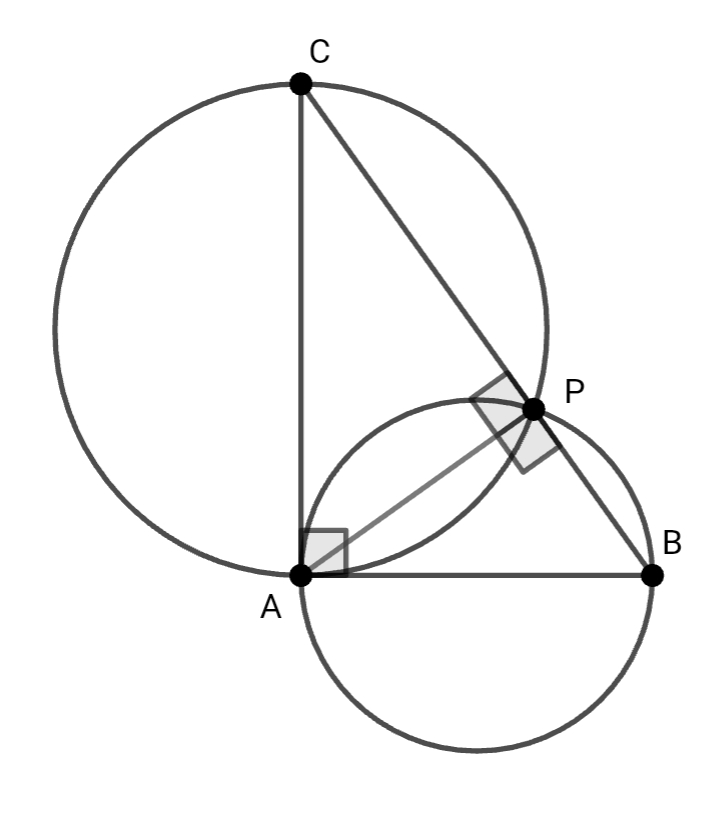
Obě odvěsny jsou průměry nových Thaletových kružnic a jejich průsečík \(P\) splňuje \(|\sphericalangle APB|=90^\circ=|\sphericalangle APC|\). Úhel \(\sphericalangle BPC\) je rovinný a průsečík \(P\) leží na přeponě trojúhelníku.
Při návratu k původnímu problému můžeme naši myšlenku aplikovat na všechny tři trojúhelníky. Tím dostaneme, že body \(B_1,B_2,B_3\) budou ležet na přeponě příslušného trojúhelníku. A jelikož trojúhelníky mají společnou přeponu \(A_2A_8\), budou body ležet nejen na jedné přímce, ale na společné úsečce.
Komentář
Úlohu většina z vás až na malé detaily hravě zvládla.
Úlohu vyřešila rychleji než by Devět věštec řekl švec. Ještě rychleji se však blížila k jeho obličeji váza bílých lilií, která se o něj roztříštila a střepy kolem něj padaly jako sníh na Vánoce. Devět zakřičel bolestí a pak se skácel k zemi omráčený.
Úloha C – Goniometrická bolest:
Určete přirozené číslo \(n\) takové, že platí: \[\sum_{i=-n}^{n}\left|\left\lceil \frac{|i|}{2}\right\rceil\sin{\left(i\cdot\frac{\pi}{2}\right)}-\left\lceil \frac{|i|+1}{2}\right\rceil\cos{\left(i\cdot\frac{\pi}{2}\right)}\right|=2054363\]
Pozn.: \(\lceil ~ \rceil\) představuje horní celou část
Řešení
Nejprve se podíváme, jak se prvky sumy liší pro různá \(n\):
\(i\) je liché (\(i = 2k+1\)), takže u kosinu dostáváme \(\cos{\left(k\cdot\pi + \frac{\pi}{2}\right)}\), což je \(0\). Naopak sinus bude nabývat hodnot \(\pm1\) (díky absolutní hodnotě můžeme nebrat v úvahu). Nakonec se ještě zbavíme zaokrouhlení nahoru. Výraz se tedy zjednoduší na: \[\left|\left\lceil \frac{|i|}{2}\right\rceil\sin{\left(i\cdot\frac{\pi}{2}\right)}-\left\lceil \frac{|i|+1}{2}\right\rceil\cos{\left(i\cdot\frac{\pi}{2}\right)}\right| = \left|\left\lceil \frac{|i|}{2}\right\rceil\sin{\left(i\cdot\frac{\pi}{2}\right)}\right| = \left\lceil \frac{|i|}{2}\right\rceil = \frac{|i| + 1}{2} = |k| + 1\]
Nyní ukážeme, že výraz bude nabývat stejných hodnot pro \(i\) a \(-i\). Jediné místo, kde se \(i\) nachází mimo absolutní hodnotu, je ve funkcích sinus a kosinus. Jelikož stále bude platit, že kosinus bude roven \(0\), zbývá nám jenom sinus. Funkce sinus je lichá: \(\sin(-x) = -\sin(x)\). Jelikož je ale celý výraz v absolutní hodnotě, na znaménku nezáleží. Pro liché \(i\) tedy platí, že výraz nabývá stejných hodnot pro \(i\) a \(-i\).
\(i\) je sudé (\(i = 2k\)), provedeme stejné úpravy jako pro liché \(i\). Jediný rozdíl bude ten, že tentokrát bude sinus roven \(0\) a kosinus bude nabývat hodnot \(\pm1\): \[\left|\left\lceil \frac{|i|}{2}\right\rceil\sin{\left(i\cdot\frac{\pi}{2}\right)}-\left\lceil \frac{|i|+1}{2}\right\rceil\cos{\left(i\cdot\frac{\pi}{2}\right)}\right| = \left|-\left\lceil \frac{|i|+1}{2}\right\rceil\cos{\left(i\cdot\frac{\pi}{2}\right)}\right| = \left\lceil \frac{|i|+1}{2}\right\rceil = \frac{|i| + 2}{2} = |k| + 1\]
Stejně jako u lichého \(i\) ukážeme, že výraz bude nabývat stejných hodnot pro \(i\) a \(-i\). Tentokrát se vynuluje sinus a kosinus je sudá funkce: \(\cos(x) = \cos(-x)\), tudíž zde rovnou dostáváme, že to platí.
Jelikož jsme ukázali, že hodnota výrazu není závislá na znaménku, můžeme sumu přepsat následovně (odečítám \(-1\), což je hodnota pro \(i=0\), protože ji nechceme započítávat dvakrát):
\[2\sum_{i=0}^{n}\left|\left\lceil \frac{|i|}{2}\right\rceil\sin{\left(i\cdot\frac{\pi}{2}\right)}-\left\lceil \frac{|i|+1}{2}\right\rceil\cos{\left(i\cdot\frac{\pi}{2}\right)}\right|-1=2054363\]
Jelikož nám vyšla hodnota \(|k|+1\) u lichých i sudých čísel, sumu lze přepsat do aritmetické posloupnosti: \[2(1+1+2+2+3+3+4+4+...+x) - 1 = 2054363\]
Abychom byli schopni určit \(x\), musíme určit, jestli je \(n\) sudé, nebo liché.
\(n\) je sudé, pro \(n\) dostáváme hodnotu \(\frac{n+2}{2}\), pro \(n-1\) hodnotu \(\frac{n}{2}\). Posloupnost tedy vypadá následovně: \[2(1+1+2+2+3+3+4+4+...+\frac{n}{2}+\frac{n}{2}+\frac{n+2}{2}) - 1 = 2054363\] \[4(1+2+3+4+...+\frac{n}{2}) +\frac{n+2}{2} - 1 = 2054363\]
Pomocí vzorečku pro aritmetickou posloupnost upravíme: \[4\frac{(\frac{n}{2} + 1)(\frac{n}{2})}{2} +\frac{n+2}{2} - 1 = 2054363\] \[n^2 + 3n = 2 \cdot 2054363\] Tato rovnice ale nemá celočíselný kořen, tudíž \(n\) nemůže být sudé.
\(n\) je liché, pro \(n\) dostáváme hodnotu \(\frac{n+1}{2}\), pro \(n-1\) hodnotu \(\frac{n-1}{2}\). Posloupnost tedy vypadá následovně: \[2(1+1+2+2+3+3+4+4+...+\frac{n-1}{2}+\frac{n-1}{2}+\frac{n+1}{2}+\frac{n+1}{2}) - 1 = 2054363\] \[4(1+2+3+4+...+\frac{n+1}{2}) - 1 = 2054363\]
Pomocí vzorečku pro aritmetickou posloupnost upravíme: \[4\frac{(\frac{n+1}{2} + 1)(\frac{n+1}{2})}{2} - 1 = 2054363\] \[n^2 + 4n + 1 = 2 \cdot 2054363\] Tato rovnice má \(2\) celočíselné kořeny: \(2025\) a \(-2029\). Jelikož \(n\) je ze zadání přirozené, máme jediné řešení \(n = 2025\).
Komentář
Ahoj, někteří z vás to vyřešili moc pěkně. Někteří jste udělali drobnou chybu, ale myšlenku jste měli dobře, to jsem strhával bod. Ti, kteří jste s tímto příkladem opravdu bojovali, koukněte na vzorové řešení :)
Kuba H.
Finťa si upravila svůj culík a pak prohodila další vázu (tentokrát s růžovými liliemi) oknem. Jako z akčního filmu proskočila za vázou oknem a přistála na nádvoří přímo na osedlaného koně.
Úloha D – Konvexní konina:
Máme čtvercovou síť a v ní souvislý (pro souvislost stačí se dotknout rohem) ohraničený útvar tvořený pouze celými čtverečky. Řekneme, že je takový útvar „čtvercově konvexní“, jestliže pro libovolné dva čtverce v tomto útvaru platí, že spojnice jejich středů leží celá v tomto útvaru. Do každého čtverečku útvaru nyní vepíšeme číslo, určující počet jiných čtverečků útvaru, do kterých se lze z daného čtverečku dostat jedním pohybem šachového koně. Nalezněte (a zdůvodněte proč další neexistují) všechny takové útvary, ve kterých jsou pouze lichá čísla. (Útvary, které jsou navzájem shodné můžete považovat za stejné).
Řešení
Prázdná množina vyhovuje zadání. Dále předpokládejme, že je útvar neprázdný. Jelikož je útvar ohraničený, jistě bude existovat čtvereček nejníže
v tomto útvaru. Tedy čtvereček, který je součástí útvaru a každý čtvereček, který leží níže již není součástí našeho útvaru. Začněme tedy s ním.
Červené vybarvení značí, že čtverec je součástí útvaru, černý křížek značí, že není. Nyní máme čtyři pole, která mohou ohrozit náš čtverec \(G1\). 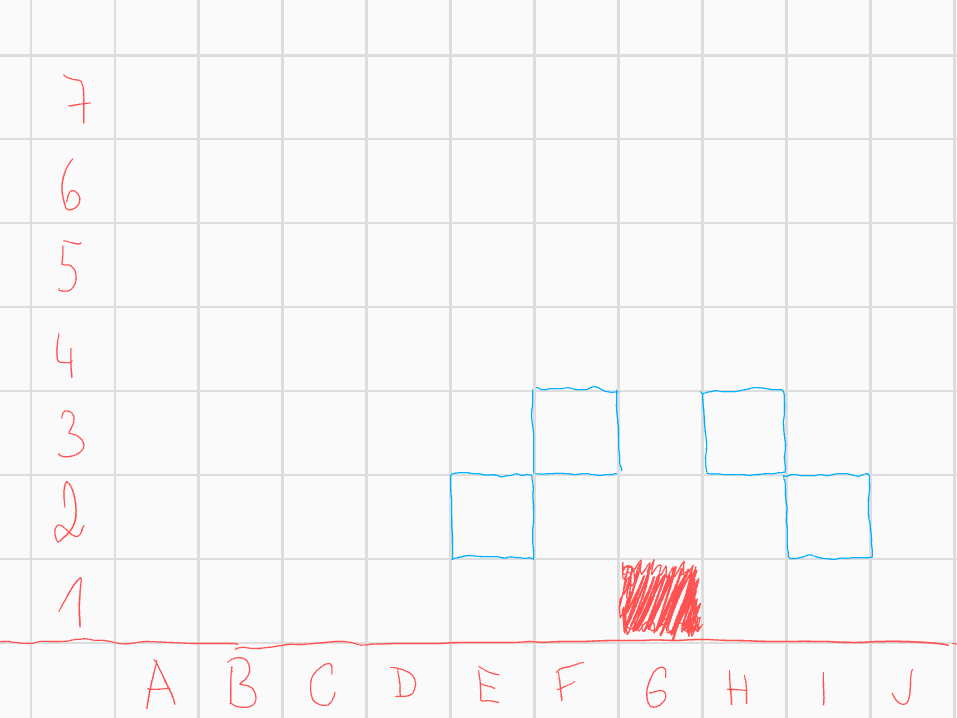 Z těchto čtyř polí musí do útvaru patřit lichý počet. Začněme tím, že rozebereme situaci, kdy do útvaru patří právě 3 z těchto polí. Pokud by do útvaru měla patřit všechna pole kromě \(H3\), dostáváme okamžitě spor, neboť spojnice středů \(I2\) a \(F3\) prochází polem \(G3\), tedy pole \(G3\) musí být součástí útvaru. Potom spojnice středů čtverců \(G3\) a \(I2\) prochází čtvercem \(H3\), což je spor s konvexností, neboť \(H3\) do útvaru nepatří. Analogicky ze symetrie nemůžeme vynechat pole \(F3\). Zbývají nám tedy 2 možnosti, ze symetrie stačí rozebrat jednu, předpokládejme tedy, že vynecháme čtverec \(I2\).
Z těchto čtyř polí musí do útvaru patřit lichý počet. Začněme tím, že rozebereme situaci, kdy do útvaru patří právě 3 z těchto polí. Pokud by do útvaru měla patřit všechna pole kromě \(H3\), dostáváme okamžitě spor, neboť spojnice středů \(I2\) a \(F3\) prochází polem \(G3\), tedy pole \(G3\) musí být součástí útvaru. Potom spojnice středů čtverců \(G3\) a \(I2\) prochází čtvercem \(H3\), což je spor s konvexností, neboť \(H3\) do útvaru nepatří. Analogicky ze symetrie nemůžeme vynechat pole \(F3\). Zbývají nám tedy 2 možnosti, ze symetrie stačí rozebrat jednu, předpokládejme tedy, že vynecháme čtverec \(I2\). 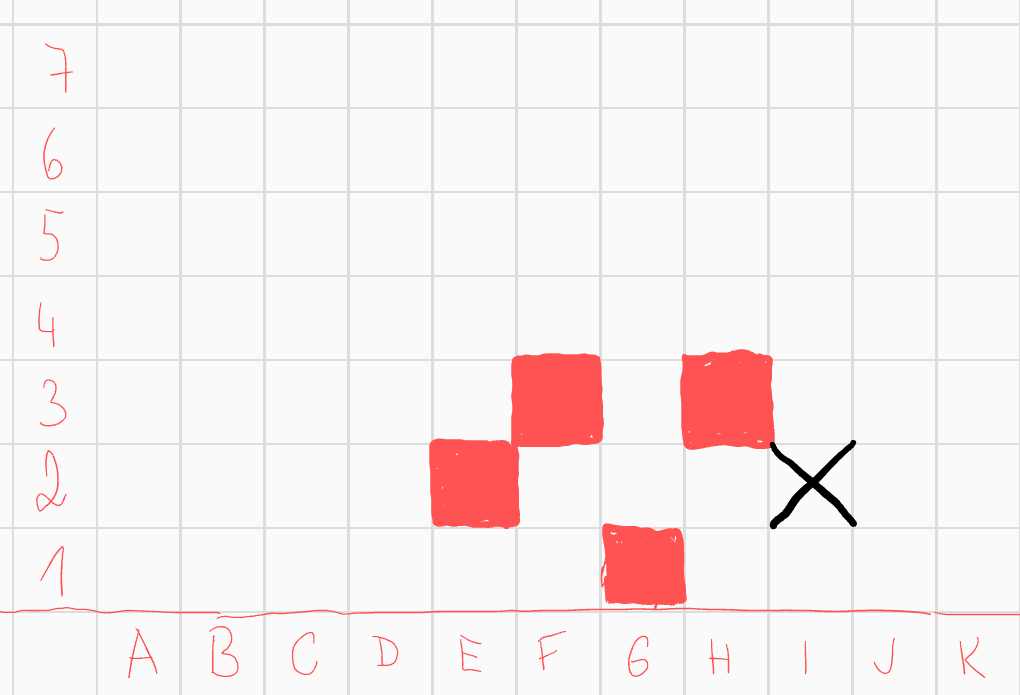 Pro konvexnost můžeme rovnou přidat a vyškrtat některá pole
Pro konvexnost můžeme rovnou přidat a vyškrtat některá pole 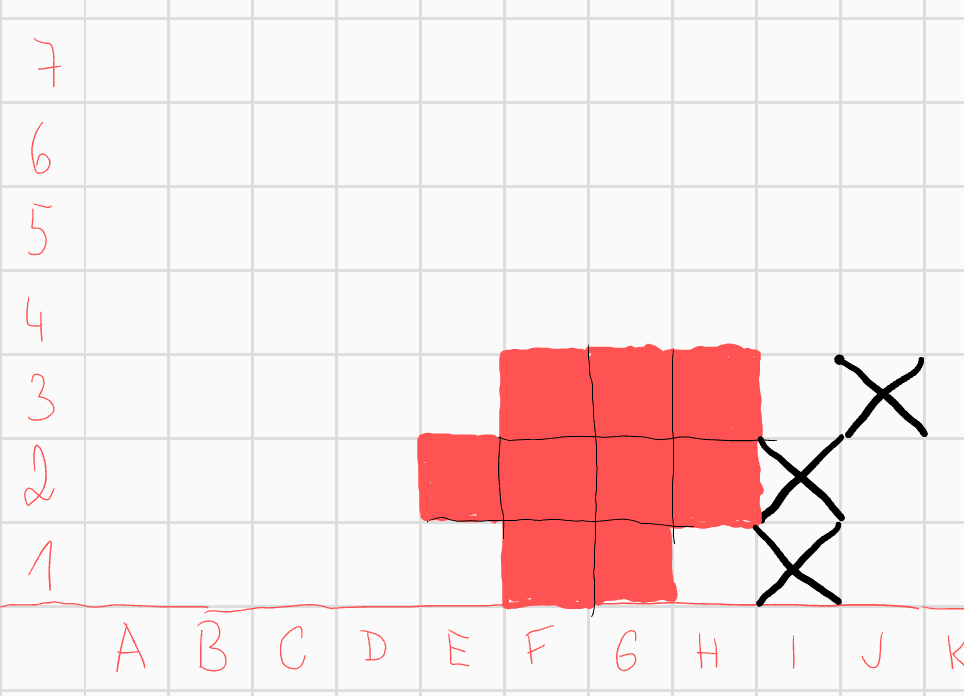 Podívejme se nyní na pole \(F1\). Zatím má číslo 2. Jediná možná pole, která ještě může ohrozit jsou \(D2\) a \(E3\). Aby mělo liché číslo, musí do útvaru patřit právě jeno z těchto polí. Pokud by to bylo \(D2\), \(E3\) by do útvaru nepatřilo a dostaneme spor s konvexností. Proto \(D2\) můžeme vyškrtnout a \(E3\) vybarvit, poté pro konvexnost vyškrtneme i \(D1\).
Podívejme se nyní na pole \(F1\). Zatím má číslo 2. Jediná možná pole, která ještě může ohrozit jsou \(D2\) a \(E3\). Aby mělo liché číslo, musí do útvaru patřit právě jeno z těchto polí. Pokud by to bylo \(D2\), \(E3\) by do útvaru nepatřilo a dostaneme spor s konvexností. Proto \(D2\) můžeme vyškrtnout a \(E3\) vybarvit, poté pro konvexnost vyškrtneme i \(D1\). 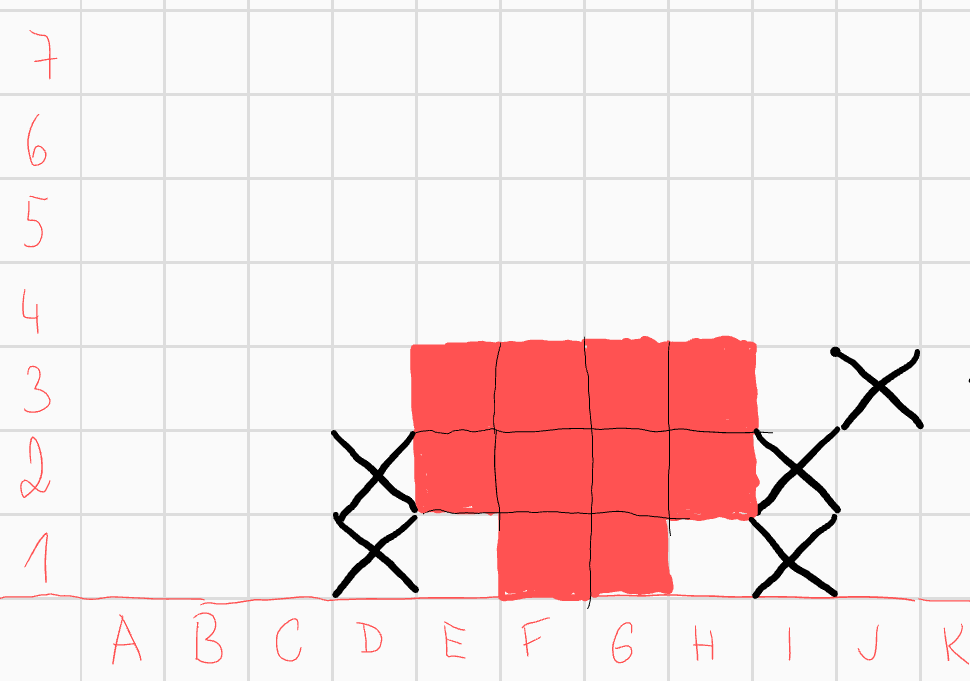 Zaměřme se nyní na pole \(E2\). Zatím má číslo 2, do útvaru tedy musí patřit právě jedno z polí \(D4\), \(F4\). Pokud by to ale bylo pole \(D4\), spojnice \(D4\) a \(H3\) prochází přes pole \(F4\), které bychom vynechali, což je spor. Tedy \(F4\) patří do útvaru a \(D4\) ne. Ze symetrie pro pole \(H2\) můžeme přidat pole \(G4\) a škrtnout pole \(I4\).
Zaměřme se nyní na pole \(E2\). Zatím má číslo 2, do útvaru tedy musí patřit právě jedno z polí \(D4\), \(F4\). Pokud by to ale bylo pole \(D4\), spojnice \(D4\) a \(H3\) prochází přes pole \(F4\), které bychom vynechali, což je spor. Tedy \(F4\) patří do útvaru a \(D4\) ne. Ze symetrie pro pole \(H2\) můžeme přidat pole \(G4\) a škrtnout pole \(I4\). 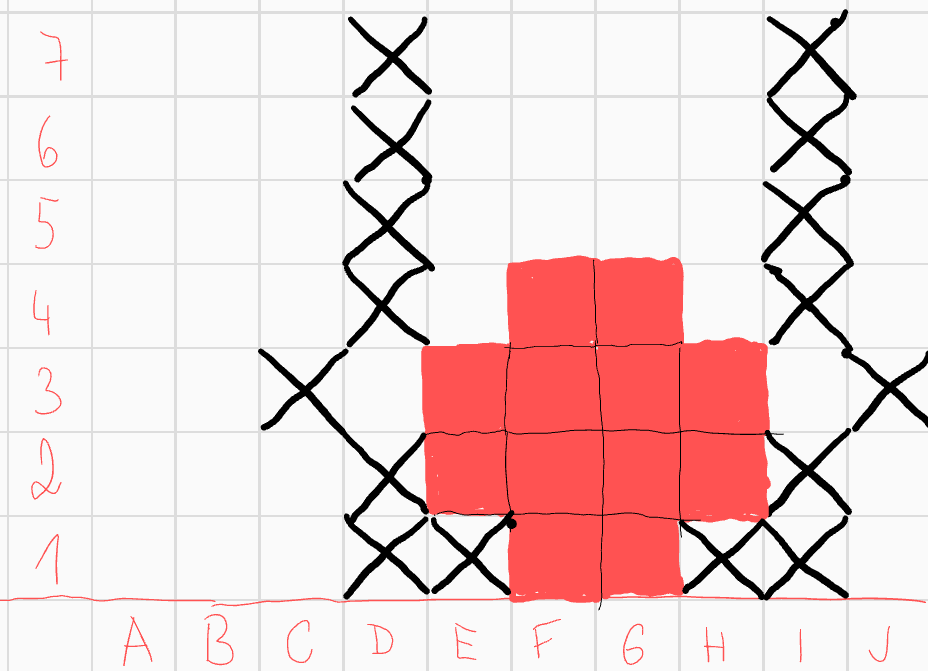 Pokud by pole \(E1\) bylo součástí útvaru, mělo by zatím skore 2. Jediné pole, které to může změnit je pole \(D3\), které by však spolu s polem \(E1\) porušilo konvexnost. \(E1\) tedy nepatří do útvaru. Analogicky pole \(H1\) nepatří do útvaru. Opět vyškrtejme nějaká pole díky konvexnosti.
Pokud by pole \(E1\) bylo součástí útvaru, mělo by zatím skore 2. Jediné pole, které to může změnit je pole \(D3\), které by však spolu s polem \(E1\) porušilo konvexnost. \(E1\) tedy nepatří do útvaru. Analogicky pole \(H1\) nepatří do útvaru. Opět vyškrtejme nějaká pole díky konvexnosti. 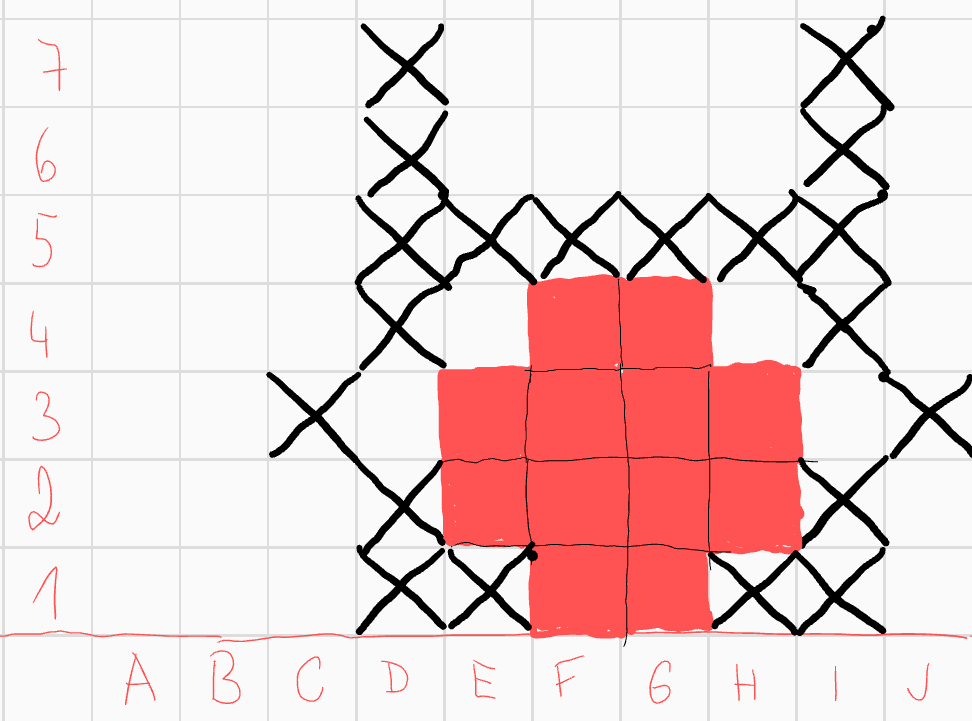 Podívejme se na pole \(E3\). Nyní má skóre 3, avšak jediné pole, které by to ještě mohlo změnit je \(H5\), které tedy nemůže patřit do útvaru. Analogicky díky poli \(H3\) nemůže do útvaru patřit pole \(G5\). Opět můžeme vyškrtat některá pole pro konvexnost.
Podívejme se na pole \(E3\). Nyní má skóre 3, avšak jediné pole, které by to ještě mohlo změnit je \(H5\), které tedy nemůže patřit do útvaru. Analogicky díky poli \(H3\) nemůže do útvaru patřit pole \(G5\). Opět můžeme vyškrtat některá pole pro konvexnost.
Pole \(F3\) má nyní číslo 2, jediné pole, které to může zachránit je pole \(H4\). Analogicky pro pole \(G3\) musíme přidat pole \(E4\). 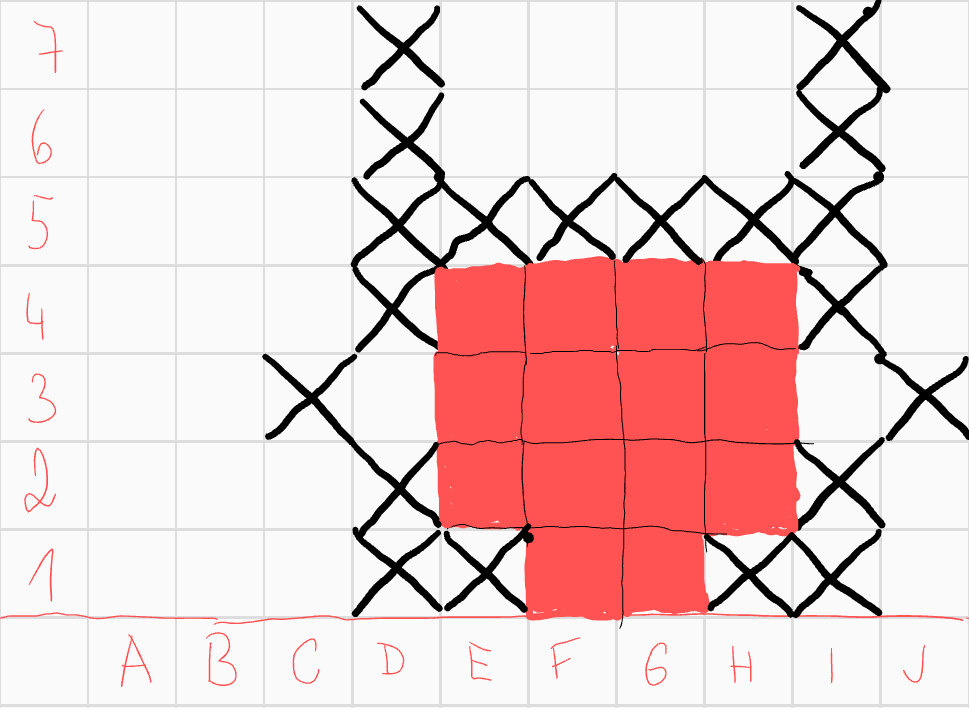 Pole \(E4\) má nyní číslo 2, avšak už nemá jak svoji hodnotu změnit, čímž dostáváme spor s tím, že jsme na začátku vybrali 3 pole, která budou naše spodní políčko ohrožovat.
Pole \(E4\) má nyní číslo 2, avšak už nemá jak svoji hodnotu změnit, čímž dostáváme spor s tím, že jsme na začátku vybrali 3 pole, která budou naše spodní políčko ohrožovat.
Dále tedy řešme variantu, kde spodní pole ohrožuje právě jedno pole. Až na symetrii máme dvě možnosti, tedy pole \(E2\) a \(F3\). Vyřešme nejprve případ, kdy jediné pole které ohrožuje \(G1\) je pole \(E2\). Rovnou můžeme z konvexnosti některá políčka přidat a některá vyškrtat. 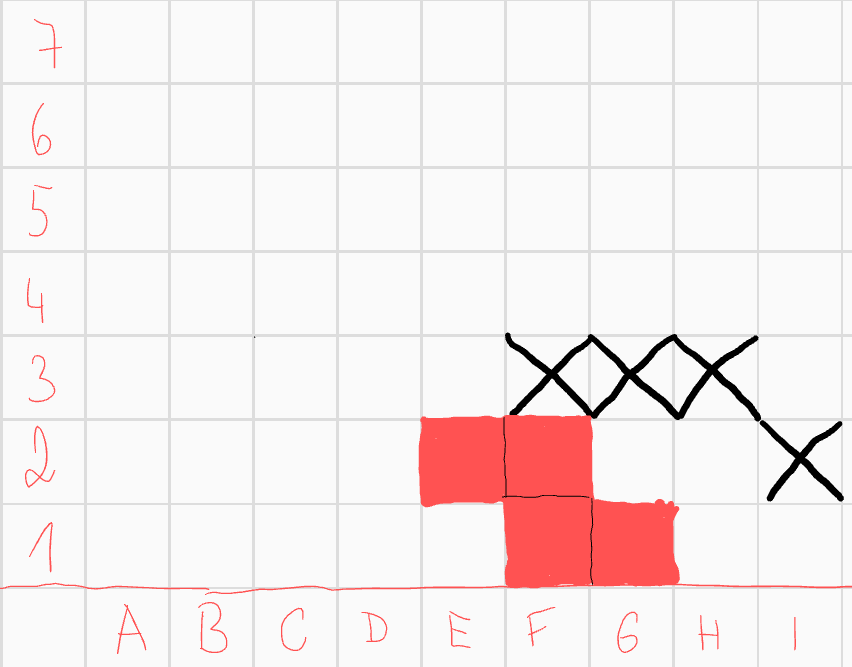 Rozdělme si tuhle variantu na dva podpřípady, podle pole \(E3\). Nejprve předpokládejme, že do našeho útvaru nepatří. To nám umožní vyškrtat všechna pole třetího řádku, díky konvexnosti. Pole \(E2\) má nyní číslo 1, což nám umožní vyškrtnout jediné další pole, které by to mohlo změnit - \(C1\).
Rozdělme si tuhle variantu na dva podpřípady, podle pole \(E3\). Nejprve předpokládejme, že do našeho útvaru nepatří. To nám umožní vyškrtat všechna pole třetího řádku, díky konvexnosti. Pole \(E2\) má nyní číslo 1, což nám umožní vyškrtnout jediné další pole, které by to mohlo změnit - \(C1\). 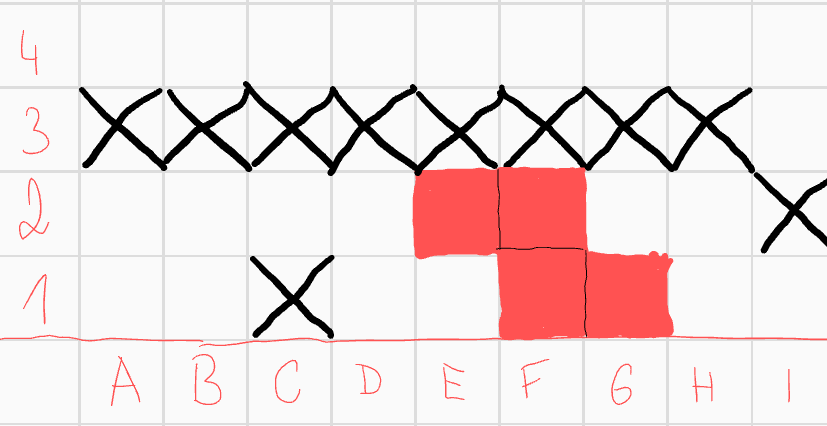 Dále si i tento podpřípad rozdělme na varianty - nejprve předpokládejme, že pole \(C2\) patří do útvaru. Konvexnost vynutí následující útvar
Dále si i tento podpřípad rozdělme na varianty - nejprve předpokládejme, že pole \(C2\) patří do útvaru. Konvexnost vynutí následující útvar 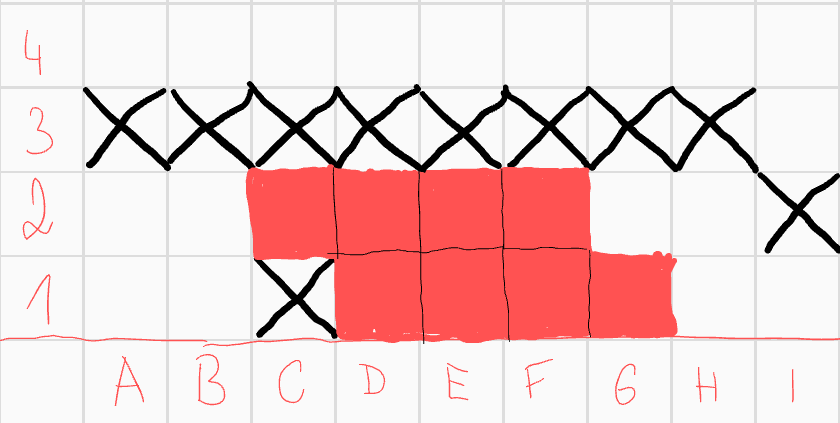 Díky poli \(D1\) nemůžeme přidat pole \(B2\), díky poli \(E2\) nemůžeme přidat \(G2\), díky poli \(F1\) nemůžeme přidat \(H2\) a díky poli \(F2\) nemůžeme přidat \(H1\). Díky konvexnosti už poté nemůžeme přidat nic. Tento útvar zároveň vyhovuje zadání.
Díky poli \(D1\) nemůžeme přidat pole \(B2\), díky poli \(E2\) nemůžeme přidat \(G2\), díky poli \(F1\) nemůžeme přidat \(H2\) a díky poli \(F2\) nemůžeme přidat \(H1\). Díky konvexnosti už poté nemůžeme přidat nic. Tento útvar zároveň vyhovuje zadání.
Nyní předpokládejme, že pole \(C2\) do útvaru nepatří. Všimněme si symetrie útvaru a toho, že kdybychom do útvaru přidali pole \(I1\), dostaneme stejnou úvahou stejný útvar jako výše. Vyškrtněme ho tedy také. Poli \(F1\) musíme přidat skóre 1, tedy přidat do útvaru pole \(D2\), nebo \(H2\). Přidáme-li pole \(D2\), z konvexnosti musíme přidat \(E1\), kterému poté musíme přidat pole \(G2\). Přidáme-li \(H2\), z konvexnosti musíme přidat \(G2\), kterému poté musíme přidat \(E1\). V obou případech jsme přidali pole \(E1\) a \(G2\), které tak musí být součástí útvaru. 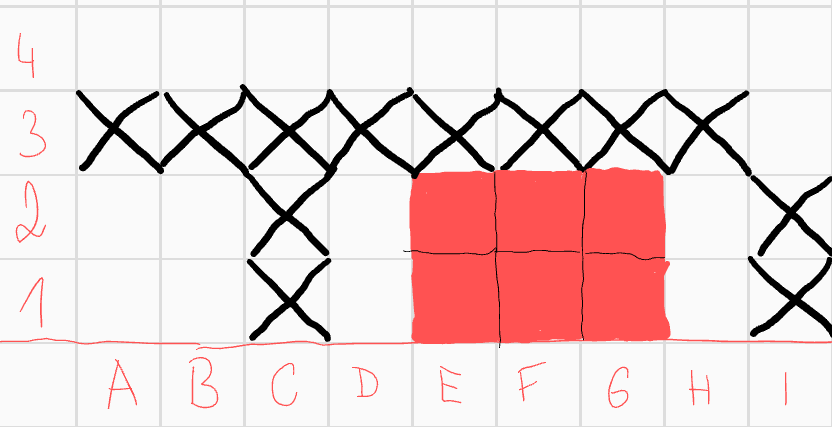 Poli \(F1\) stále chybí skóre 1. Díky symetrii můžeme předpokládat, že mu přidáme pole \(D2\). Pole \(F2\) má zatím číslo 0, musíme mu tedy přidat právě jendo z polí \(H1\), \(D1\). Přidáním pole \(H2\) dostaneme stejný útvar jako výše, přidádím pole \(D1\) dostaneme útvar, který také vyhovuje zadání.
Poli \(F1\) stále chybí skóre 1. Díky symetrii můžeme předpokládat, že mu přidáme pole \(D2\). Pole \(F2\) má zatím číslo 0, musíme mu tedy přidat právě jendo z polí \(H1\), \(D1\). Přidáním pole \(H2\) dostaneme stejný útvar jako výše, přidádím pole \(D1\) dostaneme útvar, který také vyhovuje zadání. 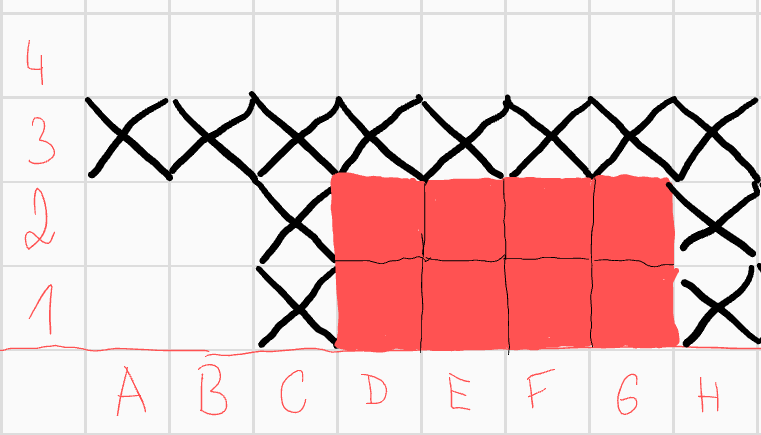 Tím jsme vyčerpali tento podpřípad.
Tím jsme vyčerpali tento podpřípad.
V druhém podpřípadě předpokládejme, že pole \(E3\) do útvaru patří. 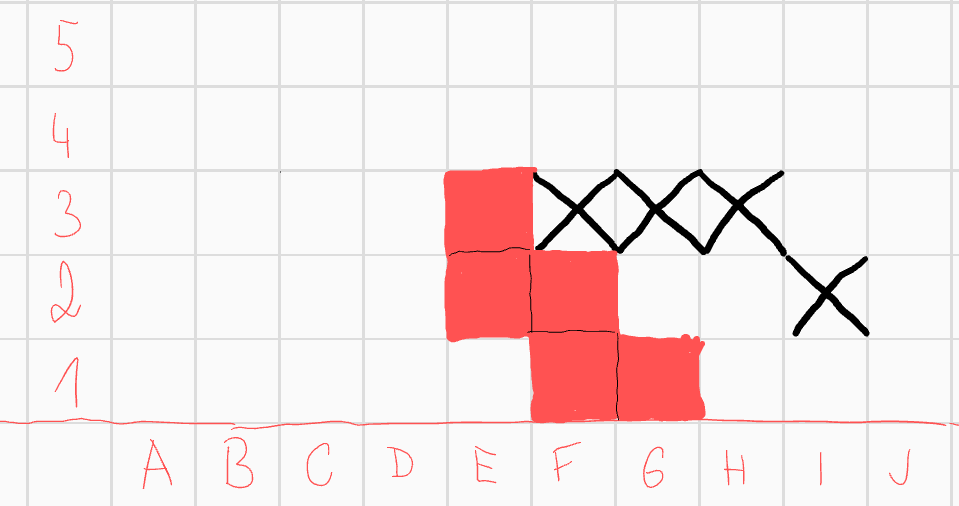 Zaměřme se na pole \(F1\). Z první části víme, že neexistuje řešení, které by obsahovalo čtverec ve spodním řádku s hodnotou 3. Proto víme, že \(F1\) musí mít hodnotu 1 a můžeme tedy vyškrtnout \(D2\) a \(H2\). Díky tomu i spoustu dalších čtverců pro konvexnost.
Zaměřme se na pole \(F1\). Z první části víme, že neexistuje řešení, které by obsahovalo čtverec ve spodním řádku s hodnotou 3. Proto víme, že \(F1\) musí mít hodnotu 1 a můžeme tedy vyškrtnout \(D2\) a \(H2\). Díky tomu i spoustu dalších čtverců pro konvexnost. 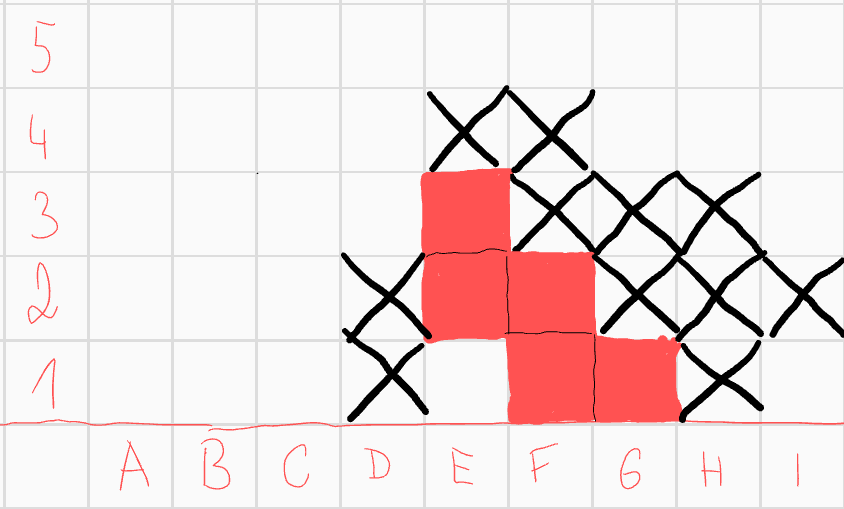 Pole \(F2\) má zatím hodnotu 0. To už může spravit poze pole \(D3\), které tedy musíme přidat, poté opět něco škrtneme z konvexnosti.
Pole \(F2\) má zatím hodnotu 0. To už může spravit poze pole \(D3\), které tedy musíme přidat, poté opět něco škrtneme z konvexnosti. 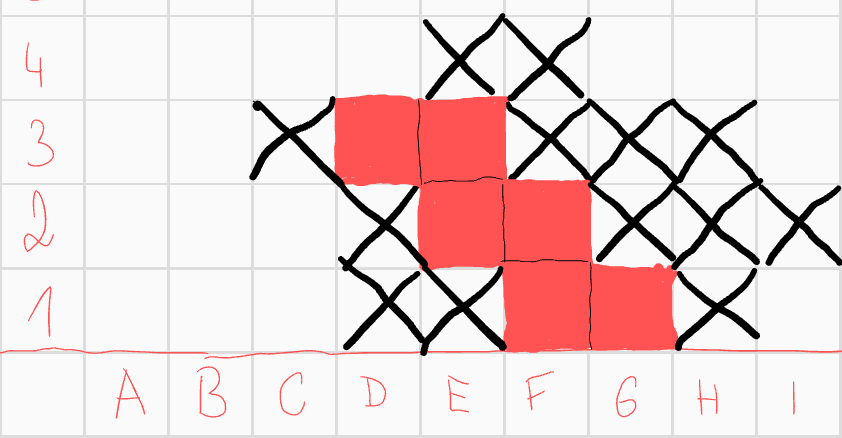 Pole \(E2\) má hodnotu 1, což by mohlo pokazit pouze pole \(D4\), můžeme ho proto vyškrtnout, s ním i pole \(C4\) pro konvexnost. Nic víc tedy přidat nemůžeme a dostáváme další útvar, který vyhovuje zadání.
Pole \(E2\) má hodnotu 1, což by mohlo pokazit pouze pole \(D4\), můžeme ho proto vyškrtnout, s ním i pole \(C4\) pro konvexnost. Nic víc tedy přidat nemůžeme a dostáváme další útvar, který vyhovuje zadání. 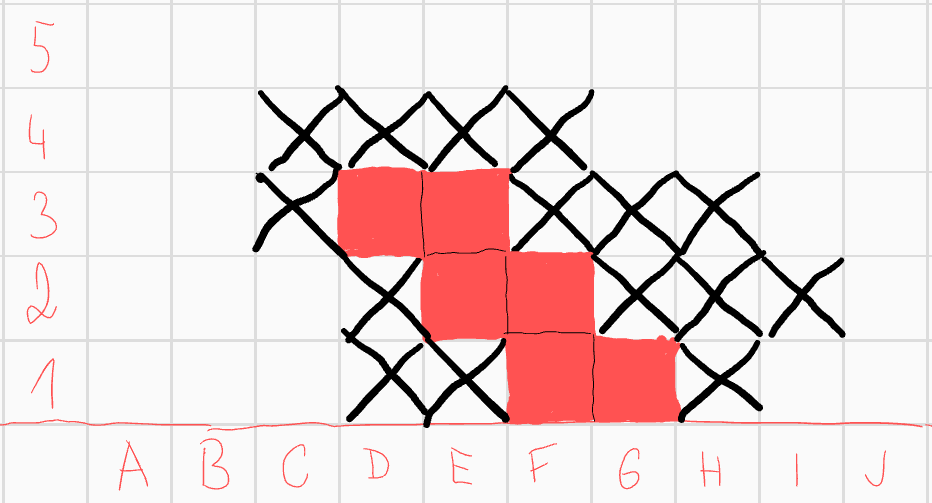
Poslední, co zbývá rozebrat je varianta, kdy úplně na začátku jediné pole, které bude ohrožovat naše spodní políčko \(G1\), bude pole \(F3\). Konvexnost nám vynutí pár polí. 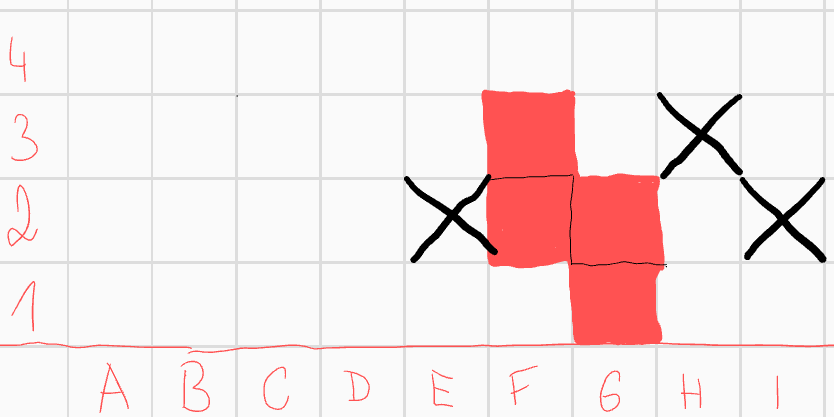 Teď přijde mega hustej argument: pokud bychom do útvaru přidali pole \(H1\), které leží ve spodním řádku, poloha pole \(F2\) vůči poli \(H1\) je stejná jako v případě, který už jsme rozebrali. Mohli bychom tedy dostat pouze řešení, která už máme, neboť každý takový útvar mohl vzniknout tak, že jsme začali polem \(H1\) ve spodní řadě a k němu přidali pole \(F2\). Pole \(H1\) tedy můžeme vyškrtnout a ze stejného důvodu i pole \(I1\) díky poli \(G2\). Rozdělme nyní i tento případ na dva podpřípady. Nejprve předpokládejme, že pole \(E3\) není součástí útvaru. Díky konvexnosti můžeme škrtnout celý sloupec \(E\).
Teď přijde mega hustej argument: pokud bychom do útvaru přidali pole \(H1\), které leží ve spodním řádku, poloha pole \(F2\) vůči poli \(H1\) je stejná jako v případě, který už jsme rozebrali. Mohli bychom tedy dostat pouze řešení, která už máme, neboť každý takový útvar mohl vzniknout tak, že jsme začali polem \(H1\) ve spodní řadě a k němu přidali pole \(F2\). Pole \(H1\) tedy můžeme vyškrtnout a ze stejného důvodu i pole \(I1\) díky poli \(G2\). Rozdělme nyní i tento případ na dva podpřípady. Nejprve předpokládejme, že pole \(E3\) není součástí útvaru. Díky konvexnosti můžeme škrtnout celý sloupec \(E\). 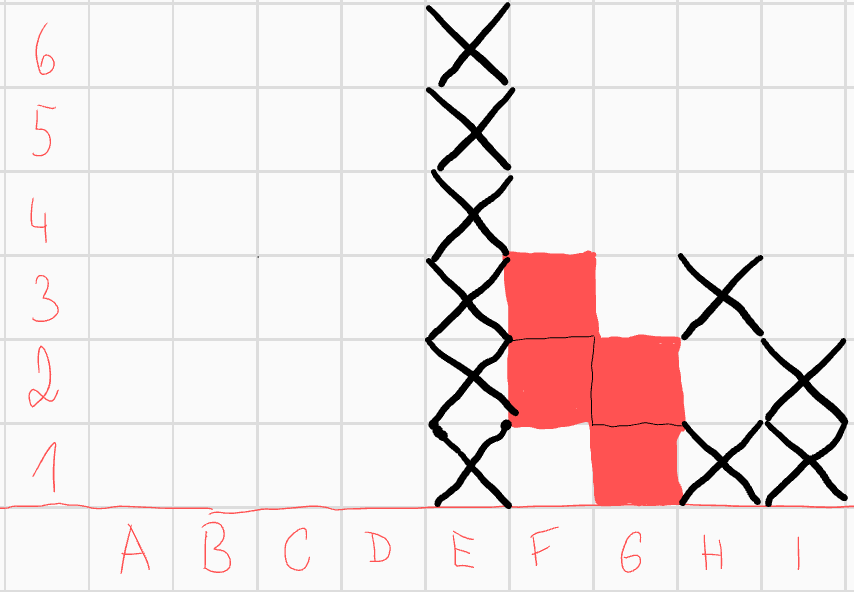 Podíváme-li se na obrázek
Podíváme-li se na obrázek zleva
(hlavu položte na pravé rameno), vyškrtnutí sloupce \(E\) hraje stejnou roli jako bychom začali se spodním sloupcem. Pole \(F2\) má jedinou možnost jak získat liché číslo - pomocí pole \(G4\), avšak při tomhle pohledu, pole \(F2\) leží ve spodním řádku a poloha vůči poli \(G4\) je již vyřešená, nemůžeme tedy dostat nic nového (upgrade předchozího argumentu). Pole \(E3\) tedy musí být součástí útvaru. Dále rozdělujme na dva podpřípady, podle pole \(H2\). Pokud by patřilo do útvaru, můžeme vyškrtnout celý sloupec \(J\) a přidat pole \(G3\) díky konvexnosti. 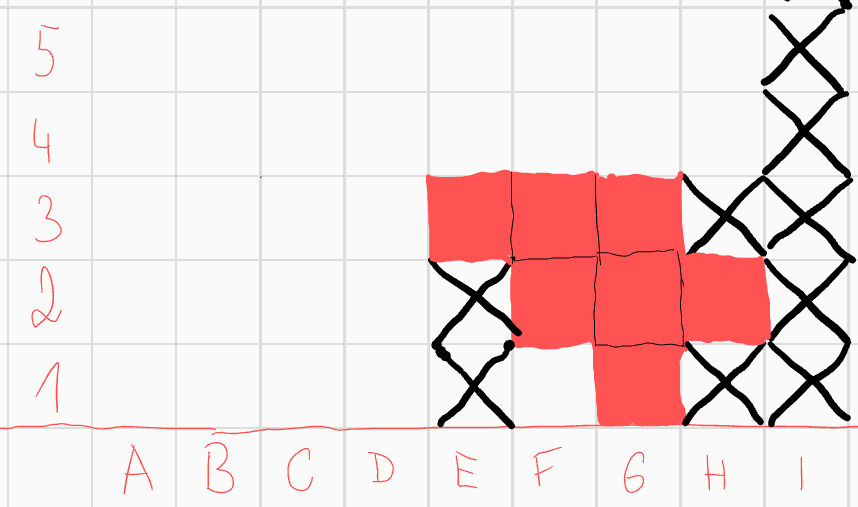 Pole \(H2\) nyní hraje roli políčka v nejspodnějším řádku při pohledu
Pole \(H2\) nyní hraje roli políčka v nejspodnějším řádku při pohledu zprava
, víme, že nemůže mít skóre 3, skóre 1 už má. Můžeme tedy škrtnout pole \(F1\) a \(G4\). Vyškrtejme některá další pole pro konvexnost. 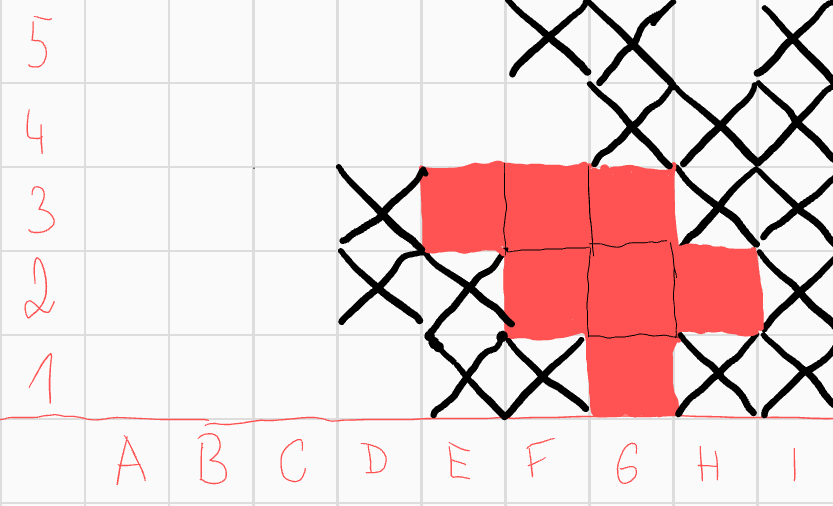 Pole \(G2\) už může ohrožovat jedině pole \(F4\), které tedy musíme škrtnout, neboť \(G2\) už má skóre 1. Z konvexnosti škrtáme i \(E4\).
Pole \(G2\) už může ohrožovat jedině pole \(F4\), které tedy musíme škrtnout, neboť \(G2\) už má skóre 1. Z konvexnosti škrtáme i \(E4\). 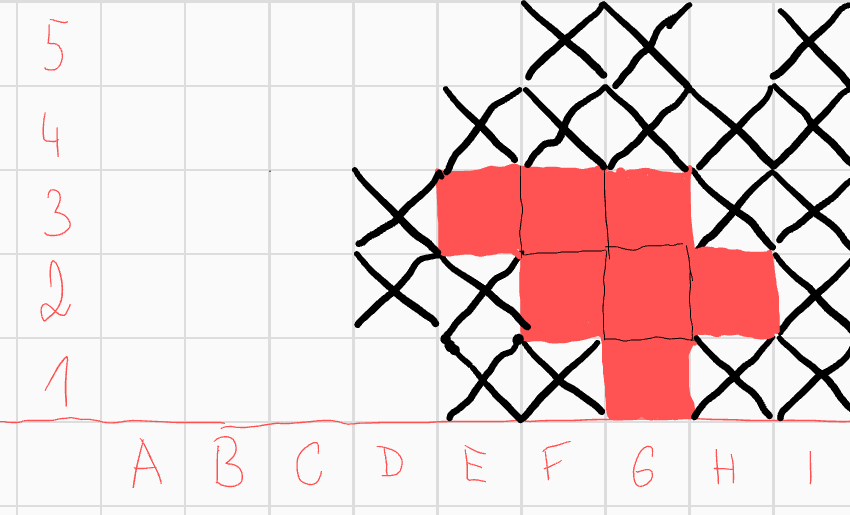 Nic už přidat nemůžeme, ale dostáváme spor například pro pole \(F2\), které má skóre 0.
Nic už přidat nemůžeme, ale dostáváme spor například pro pole \(F2\), které má skóre 0.
Druhá varianta podpřípadu je, když pole \(H2\) není součástí útvaru. Z konvexnosti můžeme vyškrtnout celý sloupec \(H\). 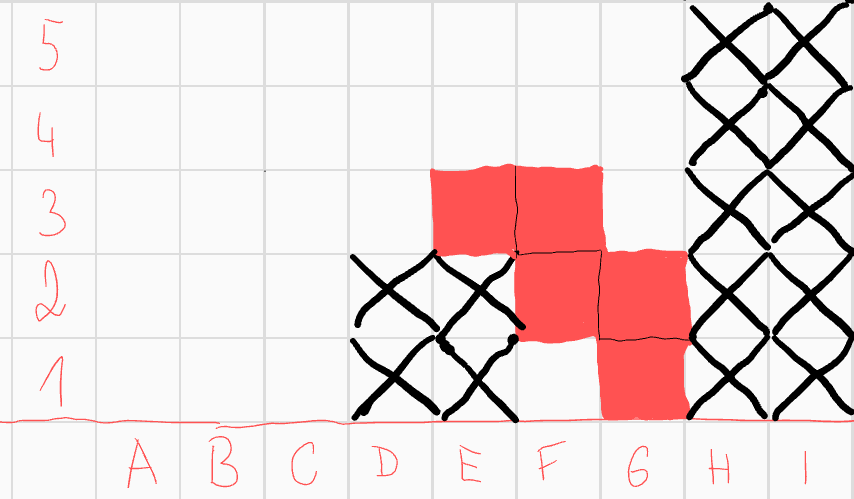 Sloupec \(G\) hraje roli spodního sloupce při pohledu
Sloupec \(G\) hraje roli spodního sloupce při pohledu zprava
, pole \(G1\) může hrát roli začátečního políčka. Jeho poloha vůči bodu \(F3\) je však ta již vyřešená (resp. s ní symetrická), proto už nemůžeme dostat žádné další řešení.
Jediná neprázdná řešení tedy až na symetrie jsou 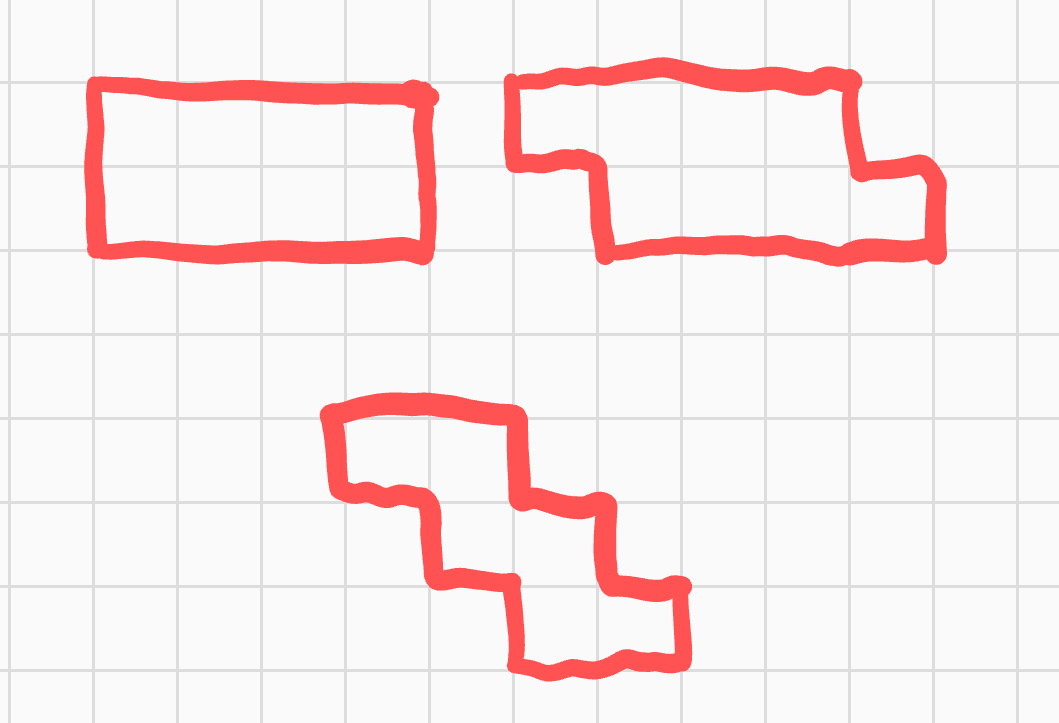
Komentář
Úlohu bylo mnohem těžší správně sepsat než ji vyřešit. Možná i proto se pouze 4 z vás pustili do řešení a pouze jedno bylo správné. Nedivím se, je to peklo na sepsání. Chválím ty, kteří aspoň začali.
Černý oř se zvedl na zadních a majestátně zaržál. Hlavy všech stráží stojících na nádvoří se otočily jejím směrem. Finťa hravě chytila oře za otěže a přeskočila s ním hradby až na velké náměstíčko, kde se před chvíli srotil dav na králův proslov. Lidí už tam bylo méně, nicméně stále tam chodili okolo stánků, oděni v pestrobarevných hábitech. Rozestoupili se před ohromnými kopyty Fintina koníka. Fintě se ještě třásly ruce, když zabrzdila koně a obrátila se na lidi na náměstí.
„Numeřané! Nenechete si rozkazovat od krále Čtvrtého a věštce Devěta! Jsou to nečistí nedobří lidé! Lžou a svrhli vám krále Třetího! Bojujte za svoje práva!“