Zadání XXXII. ročníku
1. série
Důkazy
Termín odevzdání: 20. října 2025 23:59
Na zemi se válely prázdné obaly od pizzy, dvoulitrovým PET lahvím od kofoly šlo vidět dno a u země se povaloval hustý dým různých vonných svíček, jejichž rozdílné příměsi útočily na nos, stejně jako kakofonie různobarevných outfitů bila do očí. Na zemi byl rudou rtěnkou (pozn. odstín č. 6 s názvem Bloody Mary) namalován obrovský osmiúhelník, propojený po úhlopříčkách, vložený do obrovské kružnice o průměru asi dva metry, v jehož vrcholu stála jedna z právě zmíněných vonných svíček.
Úloha 1 – Osmiobvod:
Mějme kružnici o poloměru \(1\) a do ní vepsaný osmiúhelník \(ABCDEFGH\). Čtyřúhelník \(ACEG\) je čtverec. Určete minimální a maximální obvod osmiúhelníku a formálně dokažte.
Řešení
Body \(A,C,E\) a \(G\) dělí kružnici na 4 shodné oblouky. Pokud nalezneme bod \(B\) na oblouku \(AC\), který maximalizuje/minimalizuje součet \(|AB|+|BC|\), bude to stejné platit i pro body \(D,F,H\), neboť se jedná o totožnou úlohu, pouze otočenou.
Maximální/minimální obvod budeme tedy schopni vyjádřit jako \(4(|AB|+|BC|)\) a můžeme se tedy zaměřit pouze na hledání optima pro bod \(B\).
Minimální obvod
Každé \(3\) body splňují trojúhelníkovou nerovnost: \(|AC| \leq |AB|+|BC|\). Součet \(|AB|+|BC|\) tedy nemůže nabývat menší hodnoty než \(|AC|\). Rovnost nastává v případě, kdy bod \(B\) leží na úsečce \(AC\). Zároveň však víme, že bod \(B\) musí ležet na kružnici, máme tedy jen \(2\) možnosti: \(B=A\) nebo \(B=C\). Ve výsledku tedy dojde k degeneraci osmiúhelníku na daný čtverec \(ACEG\) a minimální obvod bude:
\(4|AC| = 4\sqrt{|SA|^2 + |SC|^2} = 4\sqrt{1^2 + 1^2} = 4\sqrt{2}\)
Maximální obvod
Víme, že \(|\measuredangle ASC| = 90° = |\measuredangle ASB| + |\measuredangle BSC|\). Položme \(|\measuredangle ASB| = \alpha\), potom tedy \(|\measuredangle BSC| = 90° - \alpha\). Bod \(B\) leží na kružnici, tj \(|SB| = |SA| = 1\). Trojúhelník \(ABS\) je rovnoramenný se základnou \(AB\), pro kterou bude platit:

\[\begin{aligned} sin(\frac{\alpha}{2}) &= \frac{\frac{|AB|}{2}}{|SA|} \\ sin(\frac{\alpha}{2}) &= \frac{\frac{|AB|}{2}}{1} \\ |AB| &= 2sin(\frac{\alpha}{2})\end{aligned}\]
Podobně pro \(BC\):
\[\begin{aligned} sin(\frac{90° - \alpha}{2}) &= \frac{\frac{|BC|}{2}}{|SB|} \\ sin(\frac{90° - \alpha}{2}) &= \frac{\frac{|BC|}{2}}{1} \\ |BC| &= 2sin(45° - \frac{\alpha}{2})\end{aligned}\]
\(|AB| + |AC|\) je tedy \(2sin(\frac{\alpha}{2}) + 2sin(45° - \frac{\alpha}{2}) = 2 (sin(\frac{\alpha}{2}) + sin(45° - \frac{\alpha}{2}))\)
Pomocí vzorce pro součet dvou sinů : \(sin(x) + sin(y) = 2sin(\frac{x+y}{2})cos(\frac{x-y}{2})\), můžeme výraz dále upravit na:
\(|AB| + |AC| = 2[2sin(\frac{\frac{\alpha}{2} + (45° - \frac{\alpha}{2})}{2})cos(\frac{\frac{\alpha}{2} -(45° - \frac{\alpha}{2})}{2})] = 4sin(22,5°)cos(\frac{\alpha - 45°}{2})= 2\sqrt{2-\sqrt{2}} cos(\frac{\alpha - 45°}{2})\)
Pokud tedy nalezneme maximální hodnotu výrazu \(cos(\frac{\alpha - 45°}{2})\), nalezneme i maximální obvod celého osmiúhelníku. \(\alpha\) je z intervalu \((0°,90°)\), protože se jedná o část úhlu \(ASC\). Výraz \(\frac{\alpha - 45°}{2}\) může tedy nabývat hodnot \((-22,5°,22,5°)\). Funkce cosinus nabývá hodnot \([0,1]\), přičemž maxima (\(1\)) nabývá v hodnotách argumentu ve tvaru \(2k\pi\), pro \(k \geq 0\), \(k \in \mathbb{Z}\), což v daném intervalu \((-22,5°,22,5°)\) splňuje pouze \(0\).
Maximální obvod bude tedy v případě, kdy
\[\begin{aligned} cos(\frac{\alpha - 45°}{2}) &= 1 \\ \frac{\alpha - 45°}{2} &= 0 \\ \alpha - 45° &= 0 \\ \alpha &= 45° \end{aligned}\]
Jedná se tedy o pravidelný osmiúhelník a jeho obvod bude nabývat hodnoty \[4 \cdot (|AB| + |BC|) = 4 \cdot 2 \sqrt{2 - \sqrt{2}} cos(\frac{\alpha - 45°}{2}) = 8 \sqrt{2-\sqrt{2}}\]
Komentář
Spousta z vás úlohu vyřešila správně!!! Našla se však řešení, která nebyla úplně správná, nebo dotažená. Nejčastějším problémem bylo, že jste neprovedli pořádný důkaz (především při hledání maximálního obvodu), ale spíše jste řekli takto to prostě je! :D
Uvnitř osmiúhelníku, se šmouhami od rtěnky na růžovém topu, ležela Finťa. Hlavou u vrcholu s vonnou svíčkou s příměsí skořice a nohama směřujícíma ke speciální edici vonných svíček prodávaných ke Dni matek. V reproduktorech tématickou Bloody Mary vystřídala Abrakadabra od Lady Gagy. Celý čarodějnický výjev vysvětloval otevřený dvojlist v pohozeném teenagery oblíbeném časopise Hrom! Nacházela se v něm totiž rubrika Zoufalé manželky: Jak konečně dostat muže svých snů vysvětlující rituál, kde pomocí sledu úkonů by každá dívka do týdne měla získat kýženého muže.
Úloha 2 – Lišácké sledy:
Dokažte, že graf obsahuje uzavřený sled liché délky právě tehdy, když obsahuje uzavřenou kružnici liché délky. Délkou myslíme počet hran.
Pozn. Jestli vůbec nevíte, co je to graf, tak se podívejte na pomocný text ke 3. sérii 30. ročníku. (Najdete ho v archivu)
Pozn. Sled je libovolná posloupnost vrcholů, mezi nimiž vede hrana. Kružnice je uzavřená posloupnost vrcholů, mezi nimiž vede hrana a žádný vrchol se neopakuje.
Řešení
Pokud graf obsahuje kružnici liché délky, pak je tato kružnice zároveň uzavřeným sledem liché délky, tedy jedna implikace je triviální.
Pro tu opačnou, předpokládejme, že graf obsahuje uzavřený sled liché délky. Najděme nejkratší uzavřený sled liché délky v našem grafu. (Každý lichý sled má konečnou délku, z těchto délek vybereme tu nejmenší. Pokud tuto nejmenší délku má více sledů, vyberme si jeden libovolně.)
Ukážeme, že tento sled nejkratší liché délky je kružnice. Označme ho \(v_1,\dots v_n,v_1\). Předpokládejme tedy pro spor, že není. Potom se nějaký vrchol \(v\) v tomto sledu opakuje, tedy \(v_i=v_j\), pro \(i\neq 1\). Tento vrchol nám rozělí sled na dva uzavřené sledy, jeden z nich je \(v_i\dots v_j\), druhý je \(v_1,v_2,\dots, v_i,v_{j+1},\dots v_n\). V součtu mají lichou délku \(n\), tedy právě jeden z nich musí být liché délky, což je spor s volbou nejkratšího lichého sledu, jelikož tento nově vzniklý je kratší.
Komentář
Většina z vás si s úlohou poradila bez problému. Dokonce se mi sešlo několik různých metod důkazu. Někteří jste dokázali pouze jednu implikaci :(.
To, co ze začátku možná znělo jako obyčejná dívčí přespávačka, se brzo změnilo v noční můru. K dokončení rituálu bylo potřeba, aby jedna z přítomných dívek zarecitovala kouzelné zaklínadlo.
„Ve jménu hvězd a měsíční záře,
ať otevře se cesta v lásky tváře.
Srdce mé čisté, srdce mé v plameni,
ať láska přijde, když duše znamení.
Ať přijde ten, kdo se mnou být má,
ať duše k duši bezpečně zná.
Ne silou vázán, leč touhou svou,
ať kráčí ke mně cestou pravou.“
Finťa si na škole nenašla moc kamarádek, dalo by se jim spíš říkat followerky, protože za ní chodí, jak její stín, obletují ji jak měsíc planetu a jejich úkolem je sledovat ji na instametru a svými likey zvyšovat její oblíbenost. Většina z těchto followerek byla pro život absolutně nepoužitelná, jediná, která měla trochu rozumu v hlavě, si ale vykřičela hlasivky na koncertě Harryho Styluse, proto přednes rituálu měla na starosti jiná. Protože však nechaly okno otevřené a poskládaná báseň se trochu rozfoukala, bylo nutné ji poskládat zpátky. Nikdo si však nepamatoval, jak původní báseň zněla a tak místo ní přednesla Fintina followerka jakousi permutaci slov původní básně.
Úloha 3 – Zmutované množiny:
Máme množinu o \(n\) prvcích. K ní máme permutace \(f_1, f_2\) až \(f_m\) ne nutně různé. Kolik minimálně musí být \(m\), abychom z těchto permutací vždy mohli vybrat podmnožinu, ze které jde složit permutaci, kde se nějaký prvek z množiny zobrazí sám na sebe?
Řešení
Ozn. prvky množiny jako \(a_1, \dots, a_n\). Ukažme, že potřebujeme \(n\) permutací.
\(n-1\) nestačí - krásným protipříkladem budou permutace, které nám cyklicky prohodí všechny prvky, tj. každá permutace posune prvek \(a_i\) na \(a_{i+1}\) a \(a_n\) na \(a_1\). Pokud jich bude pouze \(n-1\), při složení se každý z prvků posune o menší počet než je \(n\), či-li se nezobrazí sám na sebe.
\(n\) už stačí - podívejme se na libovolný prvek (říkejme mu \(a\)) a zobrazme ho postupně ve všech permutacích, tj. se podívejme na \(a, f_1(a), f_2(f_1(a)), \dots , f_n(f_{n-1}(...f_1(a))...)\), těchto prvků bude přesně \(n+1\), z Dirichletova principu tam musí být alespoň dva prvky stejné. To znamená, že složení permutací mezi těmito prvky má pevný bod.
Komentář
Většina se s úlohou porvala parádně, vzorně jste ukazovali i to, že \(n-1\) nestačí!
Poslední, co Finťa slyšela, bylo: „Ve jménu hvězd vázán v plameni cestou} a pak už jen věděla, že leží na studené kamenné podlaze.“
V místnosti, kde probíhal rituál, propukla panika. Ve snaze rychle zachránit situaci jedna z dívek rychle smazala rtěnkou nakreslený osmiúhelník, druhá zavřela všechna okna, třetí skočila do rozmazaného kruhu a praštila se do lokte, čtvrtá zhasla všechny svíčky a tím se navíc v místnosti rozhostila absolutní tma. Dívky zoufale hledaly libovolné předměty na zemi, vrážely do sebe a vydávaly náhodné vysoko položené výkřiky. Dívka, co navštívila koncert Harryho Styluse ochraptělým hlasem pronesla: „To je ale nadělení.“
Úloha 4 – Nadělení:
Pro přirozené \(n > 1\) platí \((n, n-1)×(n, n-2)×...×(n, 1) = n^k\), kde \(k\) je nezáporné celé a \((a, b)\) je největší společný dělitel \(a\) a \(b\). Dokažte, že \(n\) je mocnina prvočísla.
Řešení
Tvrzení dokážeme sporem. Předpokládejme tedy, že existují dvě různá prvočísla \(p\) a \(q\), která dělí \(n\).
Podívejme se nejprve na jedno z nich a pokusme se vyjádřit, kolikrát se vyskytne v součinu na levé straně rovnosti. Víme, že \(n\) je násobkem \(p\) a \(p\) bude dělit přesně každé \(p\)-té číslo menší nebo rovno \(n\). Proto \(p\) dělí právě \(n/p - 1\) největších společných dělitelů v součinu. Pokud \(p^2\) už \(n\) nedělí, tady jsme skončili. Pokud ale ano, bude také podle stejné úvahy dělit \(n/p^2 - 1\) činitelů na levé straně.
Obecně tedy předpokládejme, že nejvyšší mocnina, v níž \(p\) dělí \(n\), je \(a\). Potom \(p^i\), \(i \leq a\) dělí právě \(n/p^i - 1\) činitelů. Abychom získali nejvyšší mocninu \(p\), která dělí levou stranu rovnice, musíme tato čísla sečíst. Dostaneme tedy
\[n/p-1 + n/p^2-1 + ... + n/p^a-1 = n(1/p + 1/p^2 + ... + 1/p^a) - a.\]
Na pravé straně máme \(n^k\). Toto číslo bude dělitelné \(p^a\) umocněným na \(k\), tedy nejvyšší mocnina \(p\), která ho dělí, je \(ak\). Jelikož se obě strany rovnice rovnají, musejí se rovnat i mocniny, v nichž je \(p\) dělí, a tak dostáváme
\[n(1/p + 1/p^2 + ... + 1/p^a) - a = ak,\] \[n(1+p+ ... + p^{a-1}) -ap^a = p^a ak,\] \[n\frac{p^a-1}{p-1} -ap^a = p^a ak.\]
Použili jsme vzoreček pro součet geometrické řady. Úplně stejnou úvahu můzeme provést i pro \(q\). Nejvyšší mocninu, ve které dělí \(n\), označme \(b\) a máme analogicky
\[n\frac{q^b-1}{q-1} -bq^b = q^b bk.\]
Vynásobením \(bq^b\), respektive \(ap^a\) dostáváme
\[nbq^b\frac{p^a-1}{p-1} -abp^aq^b = p^aq^b abk,\] \[nap^a\frac{q^b-1}{q-1} -abp^aq^b = p^aq^b abk.\]
Obě rovnice mají stejnou pravou stranu, máme tedy
\[nbq^b\frac{p^a-1}{p-1} -abp^aq^b = nap^a\frac{q^b-1}{q-1} -abp^aq^b.\] \[bq^b\frac{p^a-1}{p-1} = ap^a\frac{q^b-1}{q-1}.\]
Na levé straně rovnosti máme \(q^b\), které tak musí dělit pravou stranu. Určitě je nesoudělné s \(p^a\), vždyť \(p\) a \(q\) jsou různá prvočísla. Stejně tak je nesoudělné i se zlomkem, který je součtem geometrické řady, protože v této řadě \(q\) dělí všechny členy kromě \(1\). Zbývá tak, že \(q^b|a\). Analogicky ukážeme, že \(p^a|b\). Odtud zejména \(q^b \leq a\) a \(p^a \leq b\).
Jelikož \(p,q \geq 2\), máme \(a \geq q^b \geq 2^b\) a \(b \geq p^a \geq 2^a\), takže dohromady \(a \geq 2^b \geq 2^{2^a}\). Pro nejmenší možné \(a=1\) tato nerovnost neplatí a s rostoucím \(a\) poroste pravá strana mnohem rychleji než levá, takže nerovnost nemůže být splněna, máme spor.
Dostali jsme spor s předpokladem, kterým bylo, že existují dvě různá prvočísla dělící \(n\). Závěrem tedy je, že pokud nějaké \(n\) splňuje rovnici ze zadání, musí být mocninou prvočísla.
Komentář
S úlohou jste se popasovali moc hezky. Všechna úplná řešení měla podobnou strukturu – vyjádření \(p\)-valuací, nějaký argument s dělitelností, spor z nerovností. Někteří z vás si mysleli, že součástí kompletního postupu je i potřeba najít nějaké konkrétní řešení. Když dokazujete implikaci, není nutné se zabývat tím, jestli opravdu může nastat případ, kdy obě tvrzení jsou pravdivá.
Co se dělo nadále nás však nezajímá a raději se přesuneme za velmi zmatenou Finťou, která už se tedy zvedla ze studené kamenné podlahy. Ihned poznala, že svět, ve kterém se ocitla, není její vlastní, protože všechno bylo mnohem víc… pravidelné, ostré, přesné. Každá hrana měla přesný tvar, každá věc měla své místo. Až na ni. Finťa velice zřejmě v tomto světě přebývala, její zářivě růžový top a šachovnicové rifle bily do očí. Finťa si velice opatrně, aby si nerozmazala řasenku, otřela oči, které jí vlivem neblahých událostí trochu zvlhly, a rozhlédla se okolo. Na zemi vedle ní ležela kamenná opracovaná krychlička, na které bylo vyryto „1/2“. Kousek za ní viděla další kamennou krychličku, trochu menší, na které bylo . Protože široko daleko nebylo nic jiného, rozhodla se, že bude následovat tyto krychličky. Když se dostala ke krychličce s vyrytým číslem „1/128“ cestu k další jí přehradily obrovské zábrany z jiných krychliček.
Úloha A – Block Blast:
S použitím vyobrazených \(4\) zelených útvarů odstraňte z hracího plánu všechna zabarvená (růžová) pole. Každý z útvarů musíte použít právě jednou a nesmíte je převracet ani otáčet. Útvary vkládáte na plán postupně, pokud je zaplněna celá řada nebo sloupec, okamžitě zmizí.
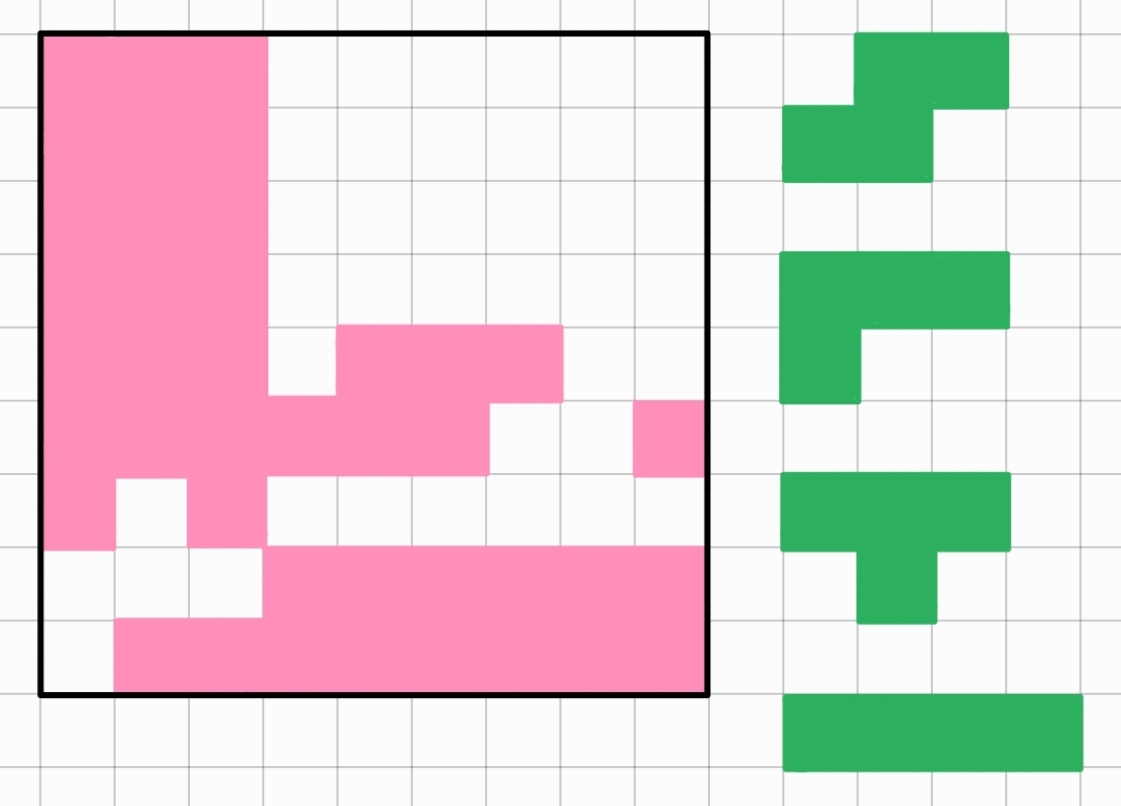
Řešení
Vzorové řešení je ilustrováno pomocí obrázků:


Přidáním tetromina tvaru S se zaplnil 6. řádek a proto zmizel.


Přidáním tetromina tvaru T se nezaplnily žádné řádky ani sloupce, tudíž žádná hrací pole nezmizela.

Přidáním tetromina tvaru L se zaplnily první 3 sloupce a poslední 2 řádky, proto zmizely.

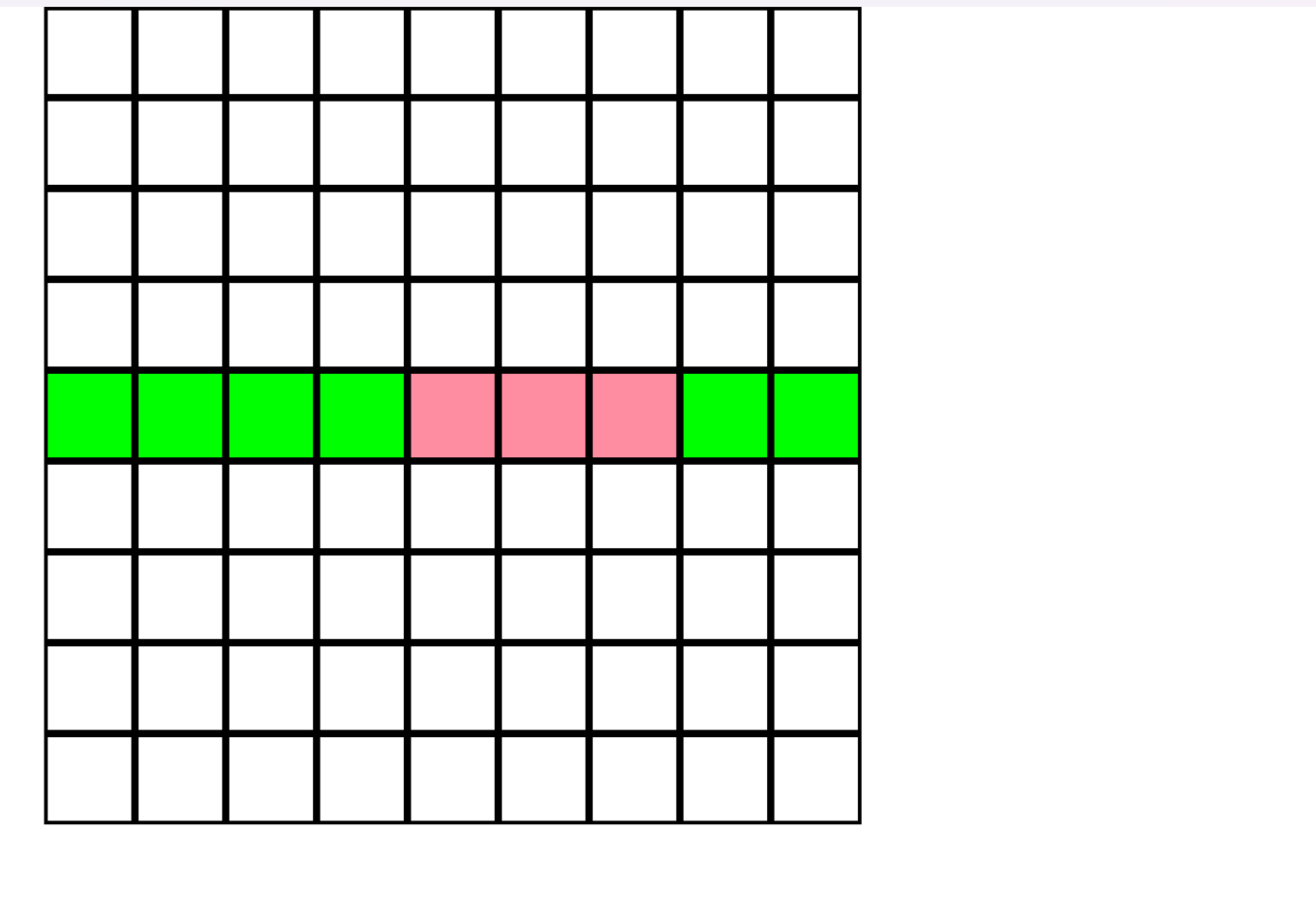
Přidáním tetromina tvaru I se zaplnil 5. řádek a proto zmizel. Na hracím plánu se již nenachází žádná zabarvená pole, tudíž jsme došli k výsledku.

Komentář
Většina z vás měla řešení naprosto správně, pár z vás bohužel nepochopilo zadání. Doufám že to již bude zřetelné ze vzorového řešení. Děkuji všem, kteří si dali práci s obrázky, moc dobře se to po vás opravovalo :)
Kuba H.
Udýchaná, ale však, veškeré kostečky se jí podařilo odstranit a cesta se jí uvolnila. Krychličky, podle kterých se orientovala se ale neustále víc zmenšovaly a byly blíž a blíž k sobě, až je v jednu chvíli skoro přestala vidět a nemusela se ani hnout z místa, aby dorazila k další. Tam Finťa narazila na krásnou zahrádku. V břiše jí zakručelo, neměla odhad, jak dlouho už v tomto světě je, ale co věděla, bylo, že má hlad. Vstoupila dovnitř a rozhlédla se po dlouhých políčkách, kde se v maticovém uskupení pěstovala všemožná zelenina. Rajčata, hrách, mrkev.
„Děvenko, nabídni si, trochu kořenové zeleniny!“ ozval se stařičký hlas.
Úloha B – Kořenová zelenina:
Najděte všechna přirozená čísla \(y\) splňující rovnici \(4^{y}-2^{y}y-4y=0\).
Řešení
Máme rovnici \(4^y-2^yy-4y=0\). Jednoduchými úpravami dostáváme \[\begin{aligned} 4^y&=2^yy+4y\\ 2^{2y}&=y(2^y+4).\end{aligned}\] Vidíme, že levá strana rovnice je tvaru \(2^{2y}\), tedy i pravá strana musí být mocnina čísla 2, proto i oba činitelé součinu na pravé straně budou mít tuto vlastnost. \[\begin{aligned} y&=2^a\\ 2^y+4&=2^b\end{aligned}\] Druhá rovnice má v přirozených číslech řešení pouze pro \(y=2\):
\(\bullet\) rovnici můžeme přepsat jako \(2^b-2^y=4\)
\(\bullet\) obecně je rozdíl \(2^m-2^n\), kde \(m \geq n\), \(m,n\in \mathbb{N}\), roven součtu mocnin dvojky \(2^k\), pro které platí \(2^n \leq 2^k < 2^m\), např. \(2^6-2^2=64-4=60=32+16+8+4\), v případě \(m-n=1\) je rozdíl roven menšiteli
\(\bullet\) v našem případě máme rozdíl 4, to nemůže být součet mocnin dvojky, proto \(2^y=4\)
Po dosazení skutečně \(4^2-2^2\cdot 2-4\cdot 2=16-8-8=0\). Tedy jediné řešení naší rovnice je \(y=2\).
Komentář
Většině z vás se úloha velmi povedla. Našli jste různé způsoby řešení, ať už jste rovnici upravovali, nebo si všimli rostoucí povahy levé strany rovnice. Ovšem spousta z vás rostoucí charakter nedokazovala, což jste mohli provést například pomocí matematické indukce.
Finťa neváhala, rovnici vyřešila a s hlasitým chřoupáním zlikvidovala několik mrkví. Hlas patřil ženě sedící na konci jednoho záhonku. Finťa si k ní přisedla na lavičku. Žena působila starší než sám čas, oči měla vlídné, záda zkroucená, jak se opírala o holi, na nohou prošoupané pantoflíčky, ruce kostnaté, že jí klouby z prstů nebezpečně vyčnívaly.
„Kde to jsme?“ zeptala se Finťa.
„Říká se tomu Numerské říši,“ odpověděla nezaujatě stařena.
„Numerská říše?“
„Nemá smysl se ptát, myslím, že to brzy pochopíš sama.“
Úloha C – Pointless úloha:
Uvažujme těleso ve tvaru koule sjednocené s kuželem, sdílejícím kruhový průřez. Průřez tohoto tělesa je na obrázku. Poloměr koule je \(1\) a výška kužele je \(3\). Určete objem tělesa.

Řešení
Jako první se zamyslíme nad tím, jak nejjednodušeji tento objem vyjádřit. Jako v zadání se na to budeme dívat pouze z boku, ale počítat budeme rovnou objem ve 3D.

Nejlehčí asi bude si těleso rozdělit podle úsečky \(XY\). Vznikne nám tak kužel (\(XYC\)) a spodní část koule. Objem kužele vypočítáme podle klasického vzorečku \(V_{kuzel}=\frac{1}{3}\pi r^2v\), kde \(r=a\) a \(v=2+c\) (protože \(|CD|=|CS|-1=2\)). Objem zbytku koule pak vypočítáme tak, že od objemu koule odečteme objem useklé úseče (vrchní), tzn.: \(V_{zbytkek koule}=V_{koule}-V_{usec}=\frac{4}{3}\pi r^3 - \frac{1}{3}\pi v^2(3r-v)\), kde tentokrát \(r\) značí poloměr původní koule, tedy \(1\) a \(v=c\) je výška úseče. Pro celkový objem tedy dostáváme: \[V=\frac{1}{3}\pi a^2(2+c)+\frac{4}{3}\pi - \frac{1}{3}\pi c^2(3-c)\] Stačí nám tedy vypočítat délky \(a\) a \(c=1-b\). Z podobnosti trojúhelníků \(ASC\) a \(XZC\) dostáváme: \[\frac{|CS|}{|AS|}=\frac{|CZ|}{|XZ|}\] \[\frac{3}{1}=\frac{3-b}{a}\] \[3a=3-b\] \[b=3(1-a)\] To si nyní dosadíme do Pythagorovy věty z pravoúhlého trojúhelníku \(SXZ\) a dostáváme kvadratickou rovnici. \[a^2+b^2=1\] \[a^2+(3(1-a))^2=1\] \[10a^2-18a+8=0\] \[5a^2-9a+4=0\] Tu si za pomoci diskriminantu \(D=(-9)^2-4\cdot 5\cdot 4=1\) jednoduše dopočítáme jako: \(a_{1,2}=\frac{-(-9)\pm \sqrt{1}}{2\cdot 5}\) a tedy \(a_1=1\) a \(a_2=\frac{4}{5}\). Můžeme si ale všimnout, že \(a\) musí být jistě menší než \(1\) a dostáváme tedy \(a=\frac{4}{5}\), \(b=3(1-\frac{4}{5})=\frac{3}{5}\) a konečně i \(c=1-\frac{3}{5}=\frac{2}{5}\). Výsledný objem tedy vychází jako: \[V=\frac{1}{3}\pi (\frac{4}{5})^2(2+\frac{2}{5})+\frac{4}{3}\pi - \frac{1}{3}\pi (\frac{2}{5})^2(3-\frac{2}{5})=\]\[=\frac{64}{125}\pi + \frac{4}{3}\pi -\frac{52}{375}\pi=\frac{192+500-52}{375}\pi =\] \[=\frac{640}{375}\pi=\frac{128}{75}\pi\]
Komentář
Začala bych tím, že opravování této úlohy mi dalo fakt zabrat. Snažila jsem se být co nejvíce spravedlivá a několikrát jsem si to kontrolovala, aby to bylo fér. Dělali jste totiž hrozně moc náhodných chyb, které se vůbec neopakovaly. Řekla bych, že to bylo většinou způsobené tím, že jste to sepisovali hodně chaoticky, nepřekontrolovali si to po sobě, nebo jste třeba vůbec nenapsali, co dosazujete do vzorečků a pak jste se v tom možná sami ztratili.. Nejčastější chybou tak bylo to, že jste do svého řešení nedali žádný obrázek.. (Můžete se podívat do pravidel, máme tam napsáno, že za to můžeme strhávat body, tak ne že si někdo bude stěžovat!) Možná vám to přijde jako blbost, ale ten obrázek fakt pomůže to řešení pochopit. Jinak moc chválím ty, co mají \(3,75\) bodů a víc! :)
Finťa se podivila. Stařenku vůbec nepřekvapilo, že Finťa neví, kde je. A současně ji ani nezajímalo, kdo Finťa je.
„Kdo jste vy?“
Stařenka se pousmála. „Já jsem Dvojka.“
„To je zvláštní jméno,“ podivila se Finťa a zadívala se na stařenčina ohnutá záda.
„Stejně jako Finťa,“ utrousila stařena a vzala z košíku jablko.
„Jak víte, jak se jmenuju?“
„Vím všechno, co vědět potřebuji.“
„Víte, jak se odsud dostanu?“
Úloha D – Ekvivalentní slova:
Mějme abecedu \(A\), která obsahuje 27 písmen. Dále mějme množinu \(S\) slov této abecedy, tedy množinu konečných posloupností písmen z \(A\) (prázdnou posloupnost nepočítáme).
Protože takových slov je opravdu hodně, budeme na těchto slovech uvažovat rovnosti \(xyxz=xz\) a \(x^2=x\), kde \(x,y,z \in S\) (tedy to jsou slova a ne písmena). V praxi to znamená, že kdykoliv ve slově bude nějaká podposloupnost \(xz\), potom slovo, co získáme tím, že nahradíme \(xz\) posloupností \(xyxz\), pro libovolné \(y\), budeme považovat za stejné slovo. A naopak, když \(xyxz\) nahradíme \(xz\), budeme též považovat slova za stejná. Stejně tak pro rovnost \(x^2=x\).
Takto se nám ztotožní opravdu hodně slov, například:
\[abc=azabc=azabzbc=azbc\]
Otázka nyní zní, kolik různých tříd slov, co jsme ztotožnili, dostaneme.
Řešení
Nejprve si lze povšimnout, že ani jedna z operací nedokáže změnit první a poslední písmeno slova (vyjma \(xx=x\), které spojí
první a poslední písmeno). Pak všechna slova délky \(2\) budou v různých třídách.
Díky příkladu ze zadání již víme, že \(abc=azbc\) (kde \(z \in S\)), tedy libovolná slova se stejným prvním a stejnými posledními dvěma písmeny jsou ve stejné třídě. Tím dostaneme, že tříd slov bude nejvýše tolik, kolik je nejvýše třípísmenných slov (ve kterých není stejné písmeno \(2 \times\) za sebou).
Díky rovnosti \(abc=abcc=abcacc=acc=ac\) však lze také přiřadit libovolnému třípísmennému slovu třídu dle jeho prvního a posledního písmene, tedy ztotožníme dvoupísmenná a vícepísmenná slova. Jinými slovy, libovolná dvě slova se stejnými počátečními a posledními písmeny jsou ve stejné třídě slov. Tříd slov je tedy tolik, kolik je dvoupísmenných slov, tzn. \(27\cdot27=729\). (pozn. jednopísmenná slova patří do příslušné třídy dle rovnosti \(a=aa\))
Komentář
Tato Déčková úloha evidentně nebyla mezi řešiteli oblíbená. Samo zadání zřejmě spoustu lidí odradilo. Osm odevzdaných řešení však mělo svou kvalitu, byť nebyla všechna správně - rovnost abc=ac byla hodně schovaná. Řešitele této úlohy mohu pochválit za snahu i správné uvažování.
„To bych věděla,“ pochlubila se Dvojka.
„Ale neřeknete mi to, protože…“
„Protože ty to ještě vědět nepotřebuješ. V Numerské říši tvůj příběh teprve začíná.“