| Časový rozestup 40 s |
Zadání XVII. ročníku
3. sada
Sada 3
Konec odevzdávání: 24. listopadu 2025 19:00
31. Oskar chce na záchod:
Oskar si chce v práci zajít na záchod, ale ten je pouze pro zaměstnance a dveře se otevírají pouze na čtyřmístný kód. Oskar ale kód zapomněl. Když přišel ke dveřím, tak si všiml, že na číselné klávesnici jsou tři čísla sedřená: \(3,1\) a \(0\) (kód se tedy může skládat pouze z těchto čísel a jedno se v něm vyskytuje dvakrát). Jaká je pravděpodobnost, že Oskar uhodne kód s těmito znalostmi na první pokus?
Řešení
Na vyřešení této úlohy stačí postupně vyčíst všechny možnosti, podobně, jako nejspíš bude muset Oskar. Jde to ale bez toho:
Nejprve si vybereme číslo, které bude dvakrát. Pro výběr tohoto čísla máme 3 možnosti
Dále nejprve umístíme zbylé dvě čísla, každé jednou:
Pro první z nich máme 4 možná místa
Pro druhé máme 3 možná místa
Na zbylé dvě místa musíme dát číslo, které je dvakrát
Celkem tedy máme \(3 \cdot 4 \cdot 3 = 36\) možností, a Oskar má šanci trefit se \(1/36\).
32. Goniometrie:
Vezměme si základní \(4\) goniometrické funkce \((\sin, \cos, \mathrm{tg}, \mathrm{cotg})\). Kolikrát se alespoň dva grafy těchto goniometrických funkcí pronikají na intervalu \[x \in \langle 0, 100\pi \rangle ?\]
Řešení
Nejjednoduší je se podívat na grafy funkcí a spočítat průsečíky. Protože hodnota \(2\pi\) je násobkem periody všech funkcí, stačí se podívat na počet průsečíků v intervalu \([0,2\pi]\).
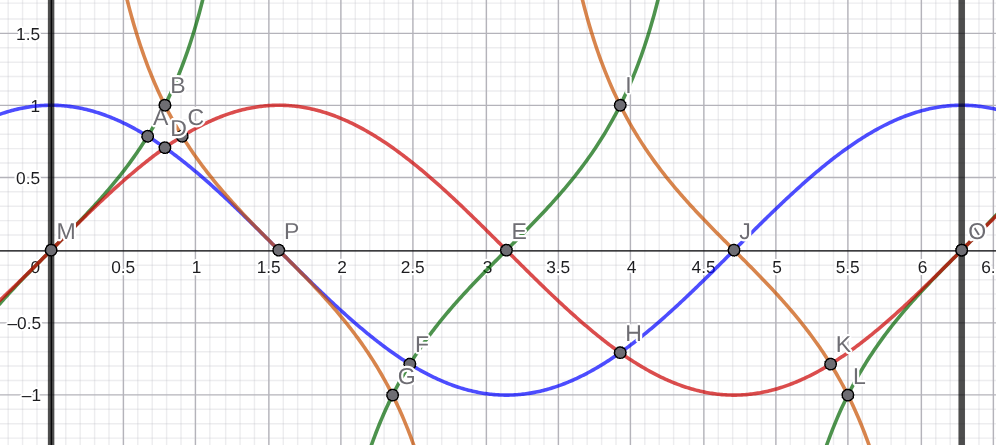
Z obrázku vidíme, že v intervalu \([0,2\pi)\) je \(14\) průsečíků, tedy v intervalu \([0,100\pi]\) jich bude \(50\cdot 14+1\) (jeden přičítáme právě pro \(x=100\pi\)). Odpověď je tedy \(701\).
33. Dřevěná deska:
Kouma chce vyrobit dřevěnou desku z deseti prken \(1:5\) (délka : šířka). Pět prken položí vedle sebe a dalších \(5\) prken položí přesně na ně otočených o \(90^\circ\) tak, že výsledná deska tvoří čtverec. Kolmo na prkna pak zatlouká hřebíky, čímž prkna spojuje. Kolik potřebuje nejméně hřebíků tak, aby všechna prkna byla spojená?
Řešení
Všech \(5\) prken z jedné (např. spodní) vrstvy se musí nějakým způsobem připojit ke druhé vrstvě, aby ani jedno neupadlo. Je však úplně jedno, k jakému prknu z druhé vrstvy prkno ze spodní vrstvy připevníme, neboť následně budeme muset spojit i prkna ze druhé vrstvy k sobě.
Pokud tedy každé z \(5\)ti prken připojíme k nějakému z druhé vrstvy, budeme mít \(5\) částí, které musíme spojit dohromady a zároveň jsme již použili \(5\) hřebíků. Na obrázku jsou prkna ze spodní vrstvy připojena k tomu stejnému z horní vrstvy a zbylé \(4\) části desky jsou \(4\) samostatná prkna.
Teď nám tedy stačí spojit zmiňovaných $5 $ částí k sobě. Zvolme si jednu část jako hlavní, a to takovou, ke které jsme připevnili alespoň \(1\) prkno ze spodní vrstvy (v našem případě to bude ta na \(1.\) obrázku). Vzhledem k tomu, že jsme prkna ze spodní vrstvy připojovali vždy pouze k jednomu z vrchní vrstvy, bude konkrétní spodní prkno zakryto jen z \(1/5\) a na zbylá \(4\) prkna z vrchní části bude stále místo. Teď jen stačí prkna na sebe vhodně položit a všechny \(4\) vedlejší části jsme schopni připevnit na naši hlavní, konkrétně na dané spodní prkno. Na to budeme potřebovat \(4\) hřebíky. Celkem jsme tedy použili \(5+4=9\) hřebíků.


34. Šifrovačka:
Řešením této úlohy je zlatý řez. Odpověď zadejte zaokrouhlenou na \(5\) platných číslic po převedení milióntinásobku do oktální soustavy.
Řešení
Ze zadání víme, že řešením je zlatý řez a jeho hodnota je \(\varphi=1,6180339...\). Takže jeho milióntinásobek bude \(1618033,9...\). Toto číslo převedeme do oktální, tedy osmičkové soustavy:
\(1618033:8=202254\) zb.1
\(202254:8=25281\) zb.6
\(25281:8=3160\) zb.1
\(3160:8=395\) zb.0
\(395:8=49\) zb.3
\(49:8=6\) zb.1
\(6:8=0\) zb.6
Máme \(1618033,..._{10}=6130161,..._{8}\). Odpověď dostáváme po zaokrouhlení na pět platných číslic: 6130200.
35. Rádi to nemyslí:
Ráďa snídá müsli a háže si do něho čísla \(1\) až \(10\), každé právě jednou. Když přihodí číslo, které je soudělné s nějakým, které už v müsli má, všechna taková čísla zmizí (včetně toho nově přidaného) a nahradí se jejich největším společným dělitelem (všech, která zmizela). Jaký může být největší součin všech čísel, které má nakonec Ráďa v müsli?
Řešení
Konečný součin může obsahovat pouze prvočinitele \(2,3,5,7\), budeme se tedy snažit je tam dostat v co nejvyšší mocnině. Určitě se nám nepodaří získat vyšší mocninu, než jaká se vyskytuje v nějakém čísle, které Ráďa do müsli hodila (pokud by se prvočíslo vyskytovalo ve více číslech, všechna by zmizela).
Můžeme tedy získat maximálně \(2^3\cdot 3^2\cdot 5\cdot 7 = 2520\). Toho opravdu lze dosáhnout, pokud čísla háže v tomto pořadí: \(1, 7, 2, 10, 4, 3, 6, 5, 8, 9\). Čísla \(1\) a \(7\) zmizet nemůžou a přihozením \(2, 10, 4\) skončíme s dvojkou. Díky \(6\) zmizí \(2\) i \(3\), takže už nám nic nepřekazí skončit s \(5, 8, 9\).
36. Na zmrzlině:
Magdalénka si s Tomášem koupili zmrzlinu. Zmrzlina je tvaru kužele, na kterém je položena polokoule o stejném poloměru. Kolem kužele je pak kornout zanedbatelné tloušťky. Domluvili se, že ona sní polovinu objemu a druhou polovinu nechá Tomášovi. Jaký podíl z původní délky hrany kornoutu má Tomášovi zůstat, jestliže úhel mezi stranami kornoutu je \(30^\circ\) a Magdalénka jí zmrzlinu rovnoměrně?
Řešení
Zmrzlina se skládá z části s kornoutem - kužele o poloměru podstavy \(r\) výšce \(h\), přičemž \(r = tg(15^\circ)h\), a polokoule o stejném poloměru \(r\). Objem zmrzliny je tedy
\[V = \frac{V_{koule}}{2} + V_{kuzele}.\]
Ze zkušenosti, i ze zadání víme, že většina zmrzliny je v kornoutu a tedy až Magdalénka dojí, bude (díky podobnosti) objem zbývající zmrzliny roven objemu kužele o výšce \(xh\) a poloměru \(xr\), kde \(x\) je odpověď na naši úlohu.
\[V_2 = \frac{1}{3}\pi (xr)^2 (xh) = x^3V_{kuzele}.\]
Tedy hledáme x, pro které \(V_2\) bude polovina \(V\).
\[V = \frac{V_{koule}}{2} + V_{kuzele} = 2x^3V_{kuzele} = 2V_2\]
\[x = \sqrt[3]{\frac{V_{koule}}{4V_{kuzele}}+ \frac{1}{2}} = \sqrt[3]{\frac{\frac{4}{3} \pi r^3}{4\frac{1}{3}\pi r^2 h} + \frac{1}{2}} = \sqrt[3]{\mathrm{tg}(15^\circ)+ \frac{1}{2}}\]
37. Ondrovy švihlé hodinky:
Ondrovy hodinky ukazují čas jako šestimístné číslo tvaru hhmmss. Pípnou mu vždy, když je číslo dělitelné \(275\) a po dělení \(9\) dává zbytek \(4\) a na pozici hodin (první dvojčíslí) jsou pouze číslice obsažené v sekundách. Kolikrát denně mu pípnou?
Řešení
275 dává po dělení 9 zbytek 5 a \(4\equiv8\cdot5 ~(\text{mod}~ 9)\), takže potřebujeme zkoumat \(275\cdot8=2200\), a tedy \(2200+9k\cdot275\). Hned vidíme, že 002200 sedí, protože na pozici hodin i sekund jsou jen nuly. Pípnou hodinky znovu?\ Nepípnou, neboť \(9\cdot275=2475\) a násobky 45 mají na místě jednotek a desítek 00, 25, 50 nebo 75, z čehož uděláme platné hodiny jen o půlnoci nebo v pět ráno. Na kalkulačce zjistíme, že po půlnoci vyhovuje jen již zmíněný případ a v pět nevyhovuje žádný (056650 je fajn, ale nemáme 66 minut).
38. Lukáš je inteligentní pozemšťan:
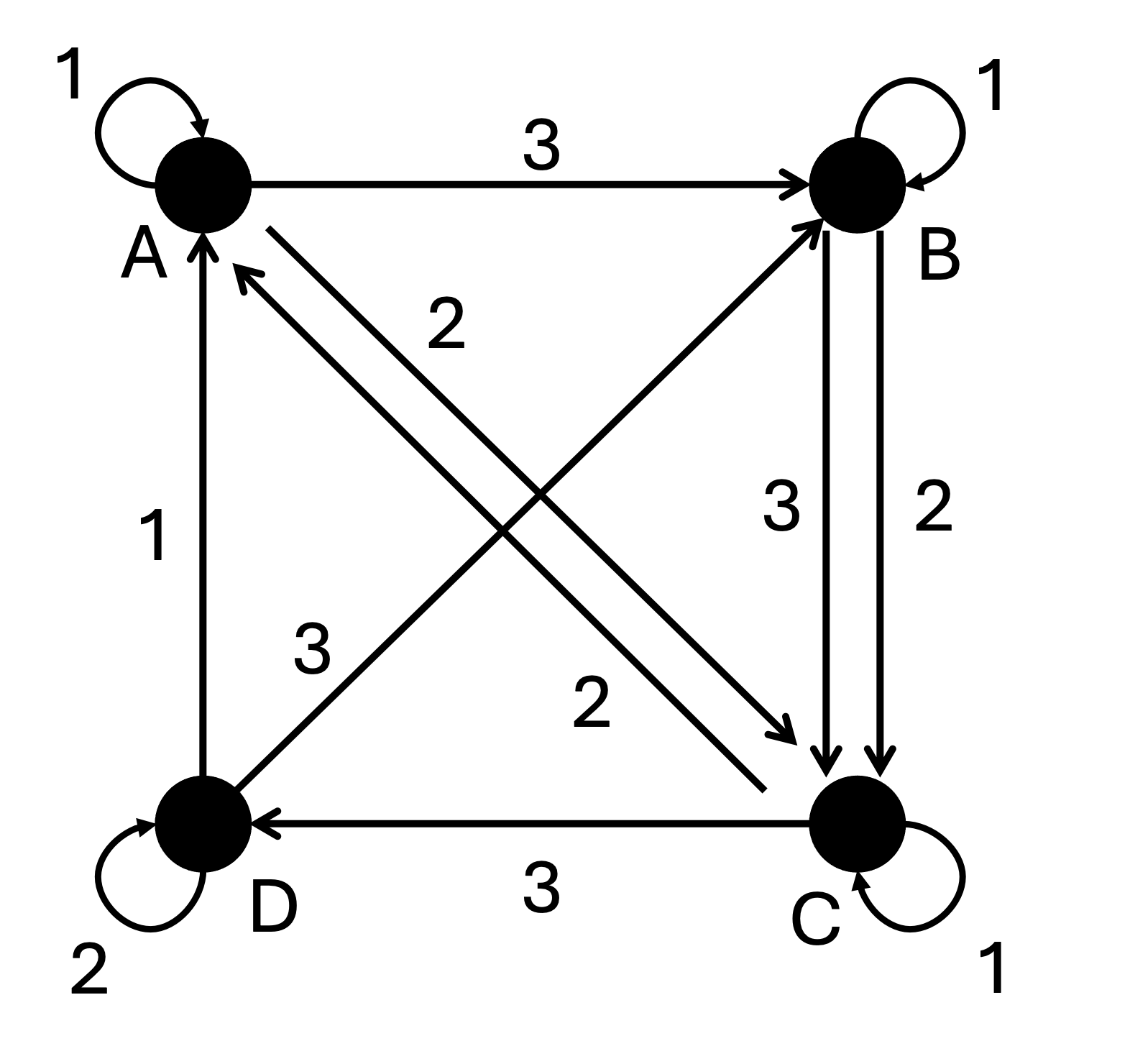
Mimozemšťané testují inteligenci pozemšťanů. Jako hádanku vytvoří bludiště propojených čtyř místností \(ABCD\), mezi kterými se testovaný subjekt může pohybovat pomocí mačkání čísel \((1,2,3)\) na ovladači, který mu dají současně s mapkou. Aby ho mimozemšťané pustili ven, musí se nacházet v místnosti \(C\) a zakřičet DEVÁTE
, pokud to ale zakřičí v libovolné jiné místnosti, nemilosrdně ho zabijí. Lukáš se ocitl mezi testovanými subjekty, na začátku mu ale nikdo neprozradil, v jaké místnosti se nachází. Lukáš je ale naštěstí inteligentní pozemšťan a našel sekvenci čísel, kterou musí zmáčknout na ovladači, aby se určitě nacházel v místnosti \(C\). Dokonce dostal pochvalu, že našel nejkratší takovou sekvenci. Zadejte ji jako řešení.
Řešení
Naším úkolem je najít tzv. synchronizační sekvenci tohoto automatu. Pomůže nám k tomu udělat si vývojový diagram. Na začátku se můžeme nacházet v libovolné z místností ABCD. Jestliže ale jednou zmáčkneme tlačítko číslo 1, tak se v tuto chvíli můžeme nacházet pouze v jedné z místností ABC, protože do místnosti D nevede šipka s číslem 1. Zkusíme to tedy rozkreslit pro všechny možnosti.
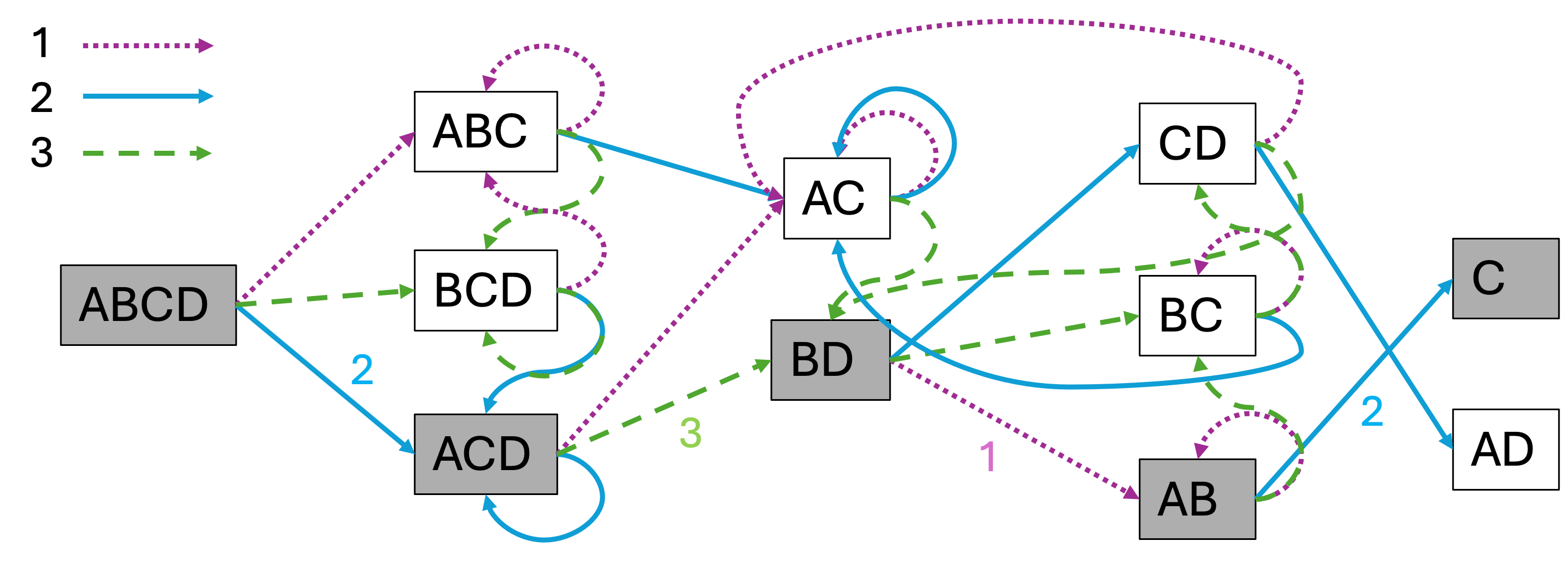
Diagram obsahuje všechny možnosti cesty délky 4. Proto řešením je zvýrazněná cesta v diagramu 2312. Kde: \[\begin{aligned} A \rightarrow C \rightarrow D \rightarrow A \rightarrow C, \\ B \rightarrow C \rightarrow D \rightarrow A \rightarrow C, \\ C \rightarrow A \rightarrow B \rightarrow B \rightarrow C,\\ D \rightarrow D \rightarrow B \rightarrow B \rightarrow C. \end{aligned}\]
39. 7-Ádická čtvrtka:
Pro každé přirozené \(N\) existuje právě jedna řada \(\sum_{n=0}^{N} a_n 7^n\), kde \(a_n \in \{0,1,\dots, 6\}\) taková, že
\[7^{N+1} \Big| 4\cdot\sum_{n=0}^{N} a_n7^n -1.\]
Napište součet všech hodnot, kterých může nabývat koeficient \(a_{2025}\).
Řešení
Postupně vyzkoušíme prvních pár hodnot.
Pro \(N=1\) dostáváme \[7^2 \Big| 4\cdot(a_07^0 +a_17^1) -1.\] To si můžeme představit jako \(4\cdot(a_07^0 +a_17^1) -1=49\cdot c\), neboli \(a_0 +7a_1=\frac{49\cdot c+1}{4}.\) Vidíme tedy, že \(49\cdot c+1\) musí být dělitelné čtyřmi, a když se na to podíváme modulo čtyři, vidíme, že \(c\) dává zbytek \(3 \mod 4.\) Vzhledem k tomu, že \(a_n\in\{0,1,\dots,6\}\), dostáváme \(c=3\). Máme tedy rovnici \(a_0 +7a_1=\frac {49\cdot 3+1}{4}=37,\) která má jediné řešení \(a_0=2\) a \(a_1=5.\)
Pro \(N=2\) dostáváme \[7^3 \Big| 4\cdot(a_07^0 +a_17^1 + a_27^2) -1.\] To si nyní opět můžeme představit jako \(7^3\cdot c=4\cdot(a_0+7a_1+49a_2)-1= (4\cdot(a_0+7a_1)-1)+4\cdot49a_2.\) Zřejmě \(7^2\) dělí levou stranu rovnice, ale i \(4\cdot49a_2\). Musí tedy dělit i \(4\cdot(a_0+7a_1)-1\). My ale z předchozího odstavce víme, že to má jediné řešení. Dostáváme tedy \(7^3\cdot c= 147+4\cdot49a_2.\) Po vydělení čtyřiceti devíti máme: \(7\cdot c= 3+4a_2,\) což má jediné řešení \(a_2=1\) a \(c=1\).
Pro \(N=3\) stejným způsobem dostaneme \(7^4\cdot c=(4\cdot(a_0+7a_1+7^2a_2)-1)+4\cdot 7^3a_3.\) Obě strany rovnice musejí být nyní dělitelné \(7^3\), což už víme, že má jediné řešení, a sice \(4\cdot(a_0+7a_1+7^2a_2)-1=7^3\). Po vydělení rovnice máme \(7\cdot c=1+4\cdot a_3\), což má jediné řešení \(a_3=5\) a \(c=3.\)
Pro \(N=4\) stejným způsobem dostaneme jediné řešení \(a_4=1\) a \(c=1\).\ Nabízí se tedy myšlenka, že pro liché \(N>1\) bude vždy \(a_n=5\) a \(c=3\) a pro sudé \(N\) naopak \(a_n=1\) a \(c=1\). Tu si nyní dokážeme pomocí indukce pro \(N\).
Bázové případy \(N=2\) a \(N=3\) byly již dokázány. Budeme nyní tedy předpokládat, že tvrzení bylo dokázáno pro \(N\in \{2,3,4,\dots,k\}\), a chceme dokázat, že pak platí i pro \(N=k+1.\)
První varianta je, že \(k\) je liché a \(k+1\) sudé. Pro \(k\) tedy už máme dokázáno, že \(4\cdot\sum_{n=0}^{k} a_n7^n -1=7^{k+1}\cdot 3\) (a \(a_k=5\)). Pro \(k+1\) tedy máme \(7^{k+2}\cdot c=4\cdot\sum_{n=0}^{k+1} a_n7^n -1=(4\cdot\sum_{n=0}^{k} a_n7^n -1) + 4\cdot a_{k+1}7^{k+1}=7^{k+1}\cdot 3+4\cdot a_{k+1}7^{k+1}.\) Po vydělení rovnice číslem \(7^{k+1}\) dostáváme \(7c=3+4\cdot a_{k+1}\), což má jediné řešení, a sice \(a_{k+1}=1\) a \(c=1,\) což je přesně to, co jsme chtěli dokázat.
Zbývá nám tedy dokázat už jen druhá varianta, a sice že \(k\) je sudé a \(k+1\) liché. Pro \(k\) tedy už máme dokázáno, že \(4\cdot\sum_{n=0}^{k} a_n7^n -1=7^{k+1}\cdot 1\) (a \(a_k=1\)). Pro \(k+1\) tedy máme \(7^{k+2}\cdot c=4\cdot\sum_{n=0}^{k+1} a_n7^n -1=(4\cdot\sum_{n=0}^{k} a_n7^n -1) + 4\cdot a_{k+1}7^{k+1}=7^{k+1}\cdot 1+4\cdot a_{k+1}7^{k+1}.\) Po vydělení rovnice číslem \(7^{k+1}\) dostáváme \(7c=1+4\cdot a_{k+1}\), což má jediné řešení, a sice \(a_{k+1}=5\) a \(c=3,\) což je přesně to, co jsme chtěli dokázat.
Každý koeficient je tedy jednoznačně určen, a protože \(2025\) je liché, dostáváme, že \(a_{2025}=5\), a tedy i celkový součet je pouze \(5\).
40. Tondův balón:
Tonda má balón ve tvaru koule o poloměru \(10\), na kterém jsou vyznačené tři body, které jsou od sebe stejně vzdálené. Pokud tyto tři body propojíme, dostaneme takový pseudotrojúhelník na sféře, jehož obvod je \(15\pi\). Spočítejte, jakou konvexní plochu na kouli tento trojúhelník vymezuje.
Řešení
Jistě to, že \(3\) body jsou od sebe stejně vzdálené v \(\mathbb{R}^3\) implikuje, že jsou od sebe stejně vzdáleny na sféře. Tedy vzniklý pseudotrojúhelník je rovnostranný a každá jeho strana má délku \(5\pi\). Jelikož má koule poloměr \(10\), její obvod je \(20\pi\), proto délka každé strany pseudotrojúhelníka je čtvrtina obvodu koule.
Po nakreslení obrázku vidíme, že jediný (až na shodnost) takový možný trojúhelník je následující:
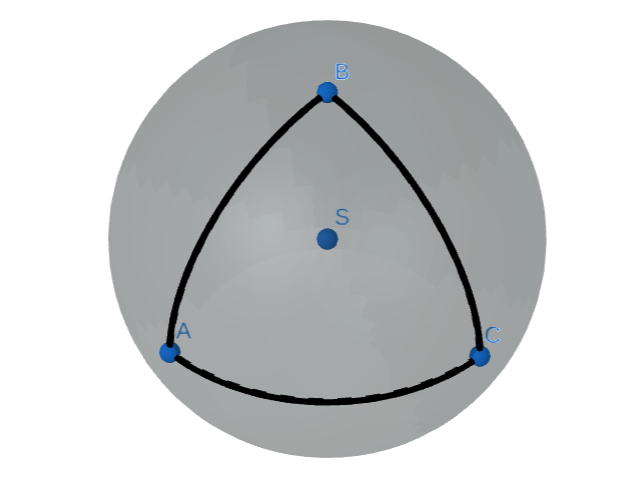
Nyní můžeme využít nějakého vztahu pro obsah sférického trojúhelníka, nebo si uvědomit, že jeho plocha zabírá osminu plochy koule. Tedy je rovna \(\frac{1}{8}\cdot4\pi\cdot r^2=\frac{\pi \cdot r^2}{2}=50\pi=157,07963\).
41. Tondova nakládačka:
Tonda má polínka, a chtěl by je naskládat do dřevníku. Dřevník je velikosti \(4\times4\). Má polínka délky \(4, 3, 3, 2, 2, 2\). Každé polínko je šířky \(1\). Kolika způsoby může Tonda dřevník naskládat, aby byl úplně plný? Všechny kusy dřeva jsou od sebe rozpoznatelné.
Řešení
Počítat všechny možnosti po jednom by bylo příliš zdlouhavé. Pokusíme se tedy najít pár symetrií, které nám ulehčí práci.
Nebudeme zvlášť počítat rozmístění obsahující polena stejné velikosti na stejných místech zvlášť. Pro každé takové jsou \(2\) možnosti, jak rozmístit polena délky \(3\), a \(3! = 6\) možností, jak rozmístit polena délky \(2\), tedy celkem \(12\) možností.
Nebudeme zvlášť počítat rozmístění, které se liší jenom otočením dřevníku. Toho můžeme docílit tak, že budeme uvažovat jenom rozmístění, ve kterých je poleno délky \(4\) v levé půlce dřevníku. Různá otočení jsou vždy \(4\). Neboť poleno délky \(4\) je jenom jedno, a v každé pozici se při každém otočení nachází na jiném místě.
Takže pro každé rozmístění dřevníku s polenem délky \(4\) v levé polovině získáme \(48\) možností!
Dále se nám bude hodit ještě jedna věc. V mnoha rozmístěních dřevníku se objeví místo velikosti \(2 \times 3\) (nebo \(3 \times 2\)), které musíme vyskládat polínky délky \(2\). Na to jsou vždy 3 možnosti:

Pro úsporu možností místo pro tyto \(3\) možnosti budeme značit hnědým blokem:

Zbývá již jen postupně zkoušet dát všechny polínka na všechna místa, kam se vejdou tak, aby to šlo dokončit. Takových konfigurací je rozumně mnoho.
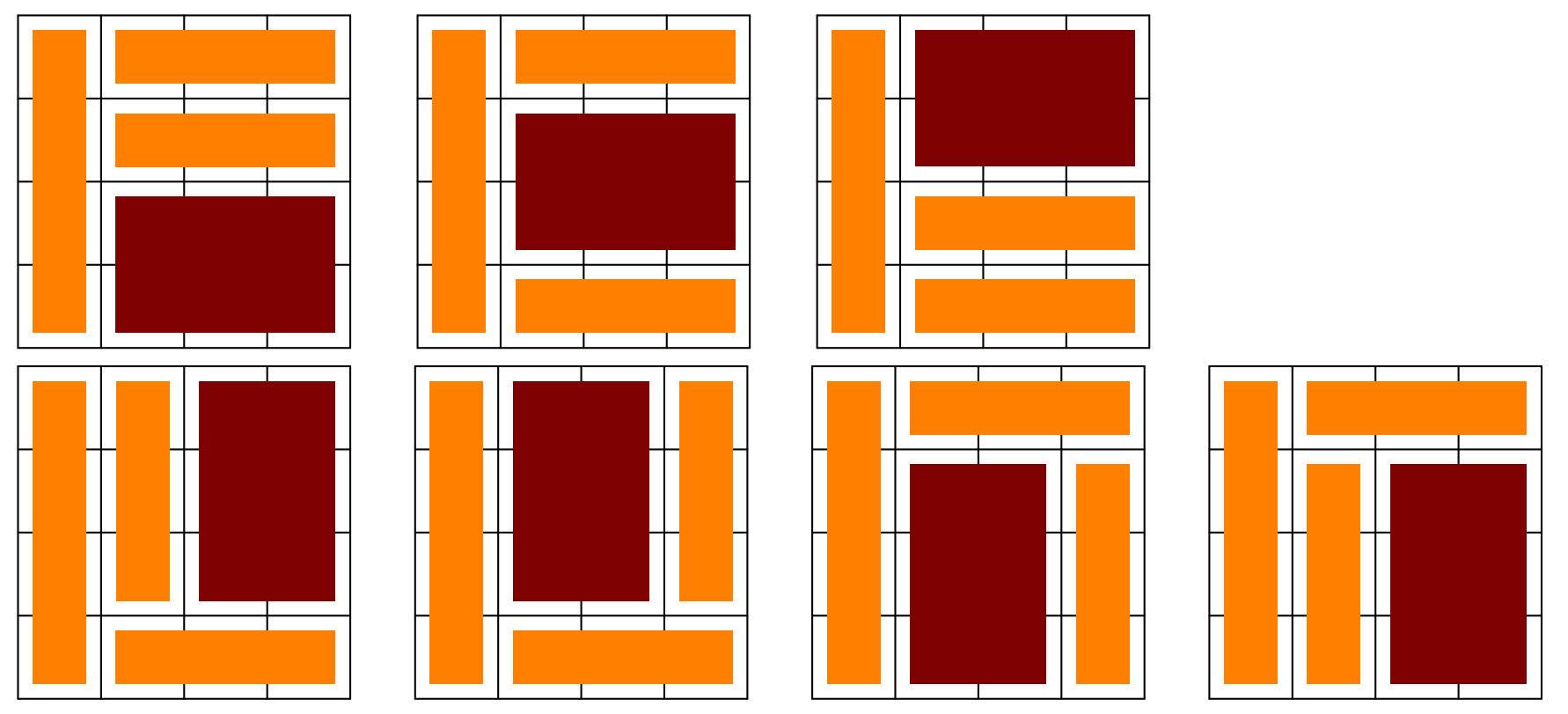
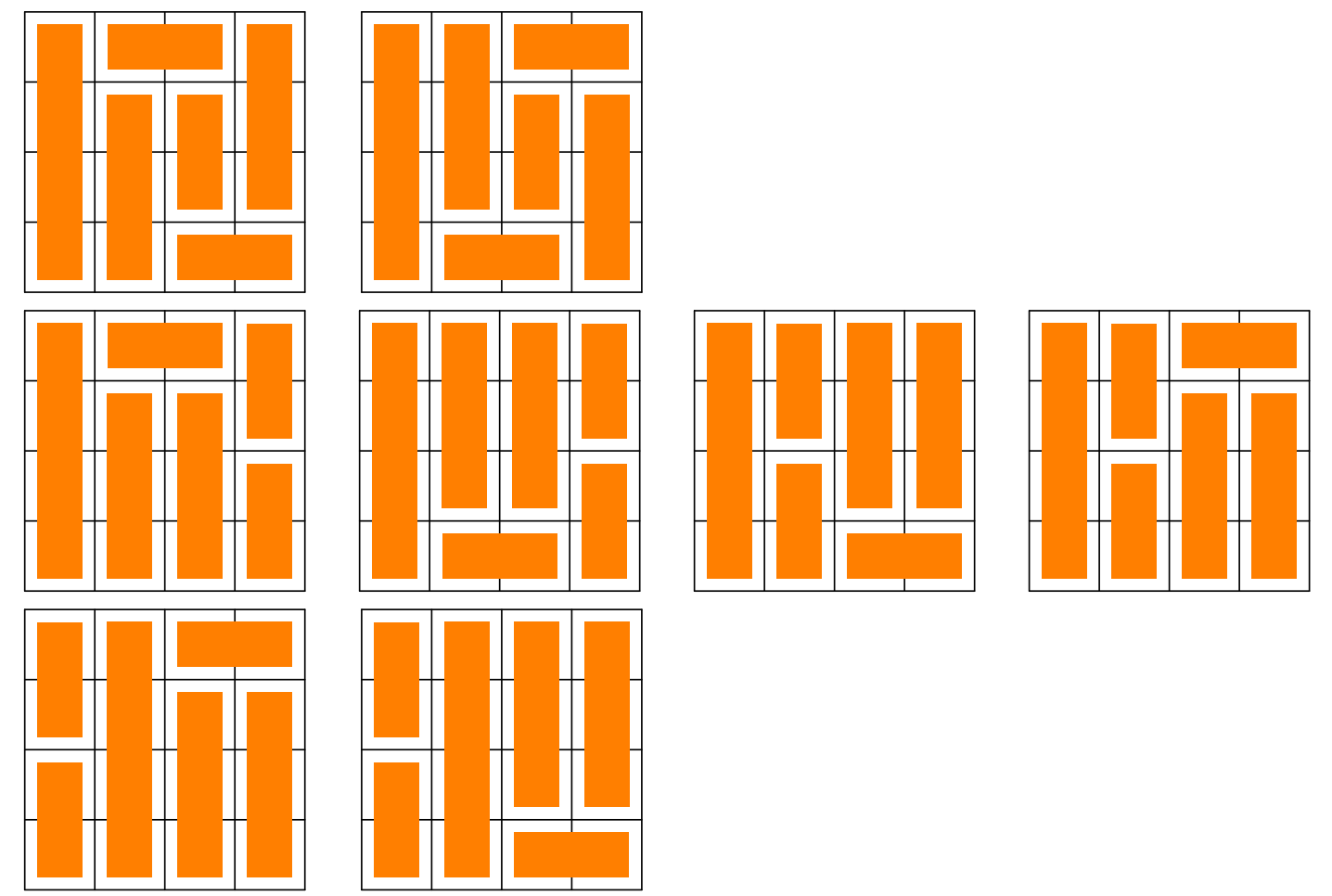
Je tedy \(7\) možností, které ještě mají hnědý blok se \(3\) možnostmi. Dále máme \(8\) unikátních možností. To je celkem \(7\cdot 3 + 8 = 29\). Jak jsme uvedli na začátku, tak každá naše možnost odpovídá \(48\) možnostem ze zadání, takže výsledkem bude \(29\cdot 48 = 1392\).
42. Alfabeta:
Máme polynom třetího stupně \(x^3+ax^2+bx+c\) a víme, že má celočíselné kořeny \(\alpha\), \(\beta\), \(\gamma\), které splňují:
\[\alpha^2\beta + \alpha\beta^2 + \alpha\beta\gamma= 28\] \[\alpha^2\beta\gamma + \alpha \beta^2 \gamma= -224\] \[\alpha^2\beta^2\gamma +\alpha^4\beta^2=-147.\]
Jako řešení odevzdejte součet \(a+b+c\).
Řešení
Ve třetí rovnici vytkneme před závorku: \[\alpha^2\beta^2(\gamma+\alpha^2)=-147\] a rozložíme \(147=3\cdot7^2\).
Kořeny musí být celočíselné, tak zkoušíme postupně dosazovat. Pokud je vytknutá část 1, vyjde \(\gamma=-148\), což nesedí po dosazení do první rovnice. Pokud je \(\alpha=\pm7\), vyjde \(\gamma=-52\) a opět spor s první rovnicí. Z \(\beta=-7\) plyne \(\alpha=\pm1, \gamma=-4\), což je v obou případech spor s první rovnicí. Ovšem \(\beta=7, \gamma=-4, \alpha=1\) platí pro všechny tři rovnice.
Nyní rozložíme polynom: \[x^3+ax^2+bx+c = (x-\alpha)(x-\beta)(x-\gamma)\] Roznásobením dostaneme vztahy \[\begin{aligned} a&=-\alpha-\beta-\gamma\\ b&=\alpha\beta+\alpha\gamma+\beta\gamma\\ c&=-\alpha\beta\gamma,\\\end{aligned}\] do nichž můžeme dosadit a získáme \[a+b+c=(-1-7+4)+(7-4-28)+(28)=-1.\]
43. Taneční soutěž:
Terka se přihlásila do taneční soutěže. Do stejné kategorie se přihlásili pouze další 2 soutěžící. Tuto kategorii hodnotí \(4\) porotci, konkrétně \(A, B, C\) a Lea. Každý z porotců nezávisle rozhodne, které představení se mu jak líbilo a následně dá každému soutěžícímu číslo od \(1\) do \(3\), podle toho, na které místo by ho umístil - každý porotce včetně Lei tedy udělí každé číslo právě jednou. O finálním umístění rozhoduje obdržený součet bodů od všech porotců (nejmenší součet vyhrává). Jaká je pravděpodobnost, že Terka vyhraje (remíza není výhra), pokud všichni porotci hodnotí vystoupení náhodně, až na Leu, která dá Terce vždy \(1\)?
Řešení
Výslednou pravděpodobnost vypočítáme jako: \[\text{pravděpodobnost}=\frac{\text{ počet možných rozdělení bodů, kdy má Terka nejméně}}{\text{všechna možná rozdělení bodů }}\] Všechna možná rozdělení bodů
Lea má jasno v tom, že dá Terce \(1\). Mezi další \(2\) soutěžící musí rozdělit \(2\) a \(3\), má tedy \(2!=2\) možnosti. Ostatní porotci musejí mezi soutěžící rozdělit \(1\), \(2\) a \(3\), mají tedy \(3!=6\) možností, jak se rozhodnout. Porotci se navzájem neovlivňují, bodování je nezávislé, celkem tedy může nastat \(2\cdot6\cdot6\cdot6=432\) různých rozdělení.
Kdy Terka vyhraje
Každý porotce rozdělí mezi soutěžící čísla \(1\), \(2\) a \(3\), tedy \(1+2+3=6\) bodů. \(4\) porotci rozdělí mezi soutěžící dohromady \(4\cdot6=24\) bodů. Pokud bude mít Terka \(8\) bodů a více, nemůže nikdy vyhrát (nejlépe dojde k remíze, a to v případě, kdy bude mít každý soutěžící \(8\) bodů (\(24:3=8\))). Zaměříme se tedy na situace, kdy má Terka mezi \(4\) a \(7\) body.
Terka má 4 body
V Tomto případě obdržela Terka samé \(1\) (pouze jedna možnost) a zároveň je zřejmé, že nikdo nemůže mít méně bodů \(\xrightarrow{}\) ve všech případech vyhrává. Každý porotce musí mezi zbylé \(2\) soutěžící rozdělit \(2\) a \(3\), každý má tedy \(2\) možnosti a celkový počet možných rozdělení, kdy má Terka \(4\) body, je \(2\cdot2\cdot2\cdot2=16\).
Terka má 5 bodů
Tato situace nastane v případě, kdy dá Terce jeden z porotců hodnocení \(2\) a ostatní \(1\). Lea dá Terce vždy \(1\), máme tedy \(3\) možnosti, od koho může Terka dostat \(2\). I v tomto případě Terka vždy vyhraje, neboť druhé nejlepší skóre by bylo \(2+2+2+1=7>5\). Dále má každý porotce zase (nezávisle na ostatních) na výběr ze dvou možností, jak body rozdělit ostatním soutěžícím, celkový počet příznivých rozdělení pro Terku tedy bude \(3\cdot2^4=48\)
Terka má 6 bodů
Zde máme již \(2\) odlišné způsoby, jak může Terka tento bodový zisk obdržet.
Hodnocení \(\{1,1,1,3\}\)
V takovémto případě je druhé nejlepší skóre stále \(2+2+2+1=7<6\), Terka tedy vždy vyhraje. Máme zase \(3\) možnosti, kdo dal Terce \(3\) a dále každý porotce vybírá ze dvou možností \(\xrightarrow{}3\cdot2^4=48\).
Hodnocení \(\{1,1,2,2\}\)
Zde je druhé nejlepší skóre \(1+1+2+2=6\) – může tedy dojít k remíze, kterou nechceme. Nejdříve se zaměřme na to, kolika způsoby může Terka dostat hodnocení \(\{1,1,2,2\}\). Budou to zase \(3\) možnosti, protože Lea dá Terce vždy \(1\) a potřebujeme vybrat jednoho porotce ze tří, který dá Terce taky \(1\). Každý porotce dále vybírá mezi \(2\) možnostmi – výsledek tedy můžeme vyjádřit jako \(3(2^4-\text{počet remíz})\), přičemž remíza nastane v případě, kdy jeden ze soutěžících obdrží samé \(3\) – to je pouze jedna možnost, avšak máme \(2\) možné soutěžící, výsledek tedy bude \(3(2^4-2)=42\).
Terka má 7 bodů
I zde jsou \(2\) možnosti, jak může Terka obdržet \(7\) bodů:
Hodnocení \(\{1,2,2,2\}\)
Aby Terka vyhrála se \(7\) body, musí mít ostatní soutěžící \(8\) a \(9\) bodů. Porotcům zbývá rozdělit hodnocení \(1, 1, 1, 2, 3, 3, 3, 3\), z čehož vyplývá, že jeden soutěžící musí dostat \(\{1,2,3,3\}\) a druhý \(\{1,1,3,3\}\) (pokud by někdo dostal tři \(3\), na druhého by zbylo moc málo bodů a Terka by nevyhrála). Uvědomme si, že pokud určíme, kdo dá \(3\) druhému soutěžícímu, je tím určeno celé rozdělení bodů (kdo nedal \(3\) \(2.\) soutěžícímu, dává ji \(3.\) a druhému dává \(1\) (Lea dává \(2\)); kdo dal \(3\) \(2.\) soutěžícímu, dává \(3.\) \(1\) (Lea \(2\))). Potřebujeme tedy vybrat \(2\) ze \(4\) porotců, kteří dají \(2.\) soutěžícímu \(3\): \[\binom{4}{2} = \frac{4!}{2!2!}=\frac{24}{4}=6\]
Hodnocení \(\{1,1,2,3\}\)
V tomto případě nám zbývá rozdělit hodnocení \(1, 1, 2, 2, 2, 3, 3, 3\). Aby měli ostatní soutěžící \(8\) a \(9\) bodů, máme \(2\) možnosti: \(\{\{2,2,2,3\},\{1,1,3,3\}\}\) a \(\{\{1,2,2,3\},\{1,2,3,3\}\}\). Nejdříve si uvědomme, že porotci \(A,B,C\) dali Terce hodnocení \(1,2,3\) \(\xrightarrow{}\) máme tedy \(3\cdot2\cdot1=6\) možností v jakém pořadí se tomu tak stalo.
V prvním případě je jasné, kteří porotci musejí dát \(2\) tomu stejnému soutěžícímu, protože zbývající porotce dal \(2\) Terce. Tím se jednoznačně určuje zbylé rozdělení, až na to, který soutěžící dostane \(\{\{2,2,2,3\}\) a který \(\{1,1,3,3\}\}\). Máme tedy \(2\) možnosti.
Ve druhém případě se zaměříme na možnosti, jak může \(2.\) soutěžící dostat \(\{\{1,2,2,3\}\). Tento počet potom vynásobíme \(2\), neboť pro \(3.\) soutěžícího to bude platit stejně a zároveň ten další vždy dostane \(\{1,2,3,3\}\}\). \(2.\) soutěžící může dostat \(1\) pouze od \(2\) porotců (těch, kteří ji nedali Terce). Pokud ji dá ten, který dal Terce \(2\), je tím jednoznačně určen zbytek, protože ten, co dal Terce \(3\), už nemůže dát \(2.\) soutěžícímu další \(1\) \(\xrightarrow{}\) dostane \(2\) a zbylí \(2\) porotci musejí dát \(3\). Pokud dostane \(1\) od toho, který dal Terce \(3\), musí ještě dostat \(\{2,3,3\}\}\), přičemž všichni $3 $ zbývající porotci mají k dispozici \(3\), ale jen dva mají k dispozici \(2\) \(\xrightarrow{}\) máme \(2\), kdo dá \(2\), ostatní dají \(3\). Celkem tedy Terka vyhraje s hodnocením \(\{1,1,2,3\}\) v \(6(2 + 2(1+2))=48\) případech.
Celkem Terka vyhraje v \(16+48+48+42+6+48=208\) případech ze \(432\), pravděpodobnost je tedy \(\frac{208}{432}=\frac{13}{27}\).
44. Pythagorova procházka:
Štěpán s Ondrou musí na ranní přednášku z algebry. Chodí po celočíselných mřížových bodech kartézské soustavy souřadnic, kde jejich dům se nachází na souřadnici \((0,0)\) a škola na \((20,20)\). Chodit mohou pouze po přeponách pravoúhlých trojúhelníků s vrcholy v mřížových bodech a jejich cesta musí mít celočíselnou délku, souřadnice své polohy mohou pouze ostře zvyšovat (tzn. nesmí jít vůbec dolů nebo doleva, ani kolmo nahoru, či vodorovně doprava). Kolika způsoby se mohou dostat do školy?
Řešení
Předpokládejme, že jednotlivé kroky jsou celočíselné, tedy trojúhelníky tvořené krokem a odpovídajícími úsečkami na osách x a y jsou Pythagorejské. Potom délky odvěsen musí být nejvýše 20, přesněji se musejí nasčítat na 20 a to jak ve směru x, tak ve směru y. Pythagorejské trojúhelníky s oběma odvěsnami menšími než 20 jsou
\[(3, 4, 5), (5, 12, 13), (8, 15, 17),\] kde první dvě čísla jsou odvěsny a třetí přepona.
Snadno zjistíme, že jediný způsob, jak vybrat několik trojúhelníků, jejichž souřadnice se správně nasčítají je vybrat \((5, 12, 13)\) a \((8, 15, 17)\). Cestu do školy poté můžeme utvořit čtyřmi způsoby, a to skrz bod \((5,12)\), bod \((12,5)\), bod \((8,15)\) a bod \((15,8)\).
Podrobný důkaz, že stačí uvažovat pouze celočíselné trojúhelníky s odvěsnami rovnoběžnými osám ponecháváme kuriozitě čtenáře.
45. Anička na třešních:
V sadu stojí \(6\) třešní o obvodu kmene \(10\pi\) cm. Středy jejich kmenů jsou v mřížce \(3\times2\), sousední středy jsou dva metry od sebe. Anička chce natáhnout provázek, na který kladkou připne košík. Provázek povede kolem každého stromu. Aby provázek držel, musí vést napnutý aspoň kolem poloviny obvodu kmene, ne však okolo celého obvodu, to by strom škrtil. Konec provázku Anička naváže na začátek. Jak nejméně dlouhý provázek bude potřebovat? Odpověď zadejte v metrech zaokrouhlených na \(5\) desetinných míst. Na obrázku je příklad povoleného obmotání stromů v mřížce \(2\times2\).
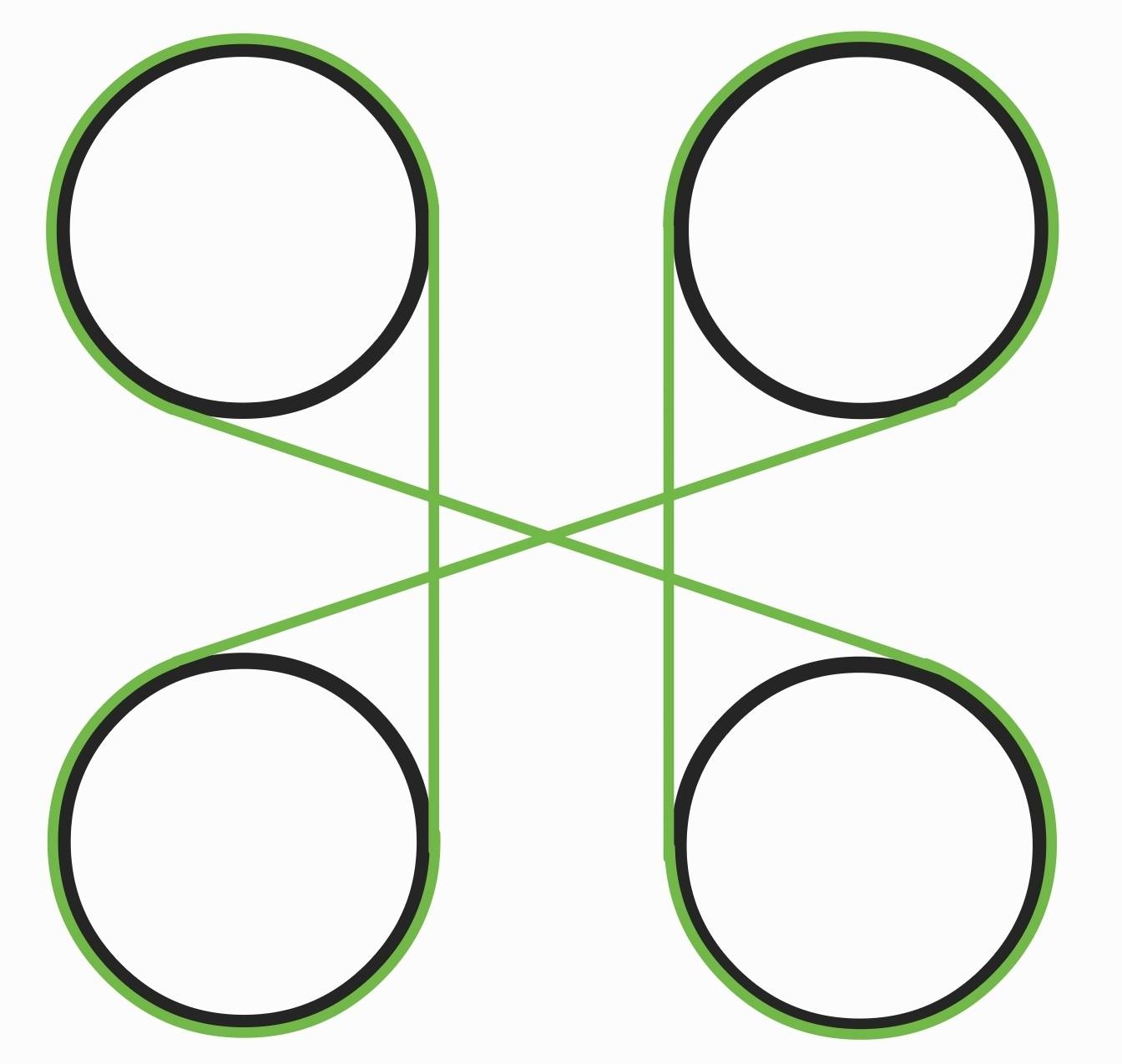
Řešení
Nejdříve určíme nejkratší cestu a poté vypočítáme její délku. V ideálním případě by nejkratší cesta byla tvořena pouze přímými 2,m dlouhými hranami, ale to kvůli podmínce vedení provázku kolem více než půlky a méně než celého obvodu kmene není možné. Navíc díky požadavku nejkratší cesty stačí uvažovat pouze cesty o šesti hranách. Chceme co největší počet přímých hran, ale musíme pohlídat i rozdíl délek ostatních možných cest a přičítání částečných obvodů kmenů. Máme následující kandidáty:
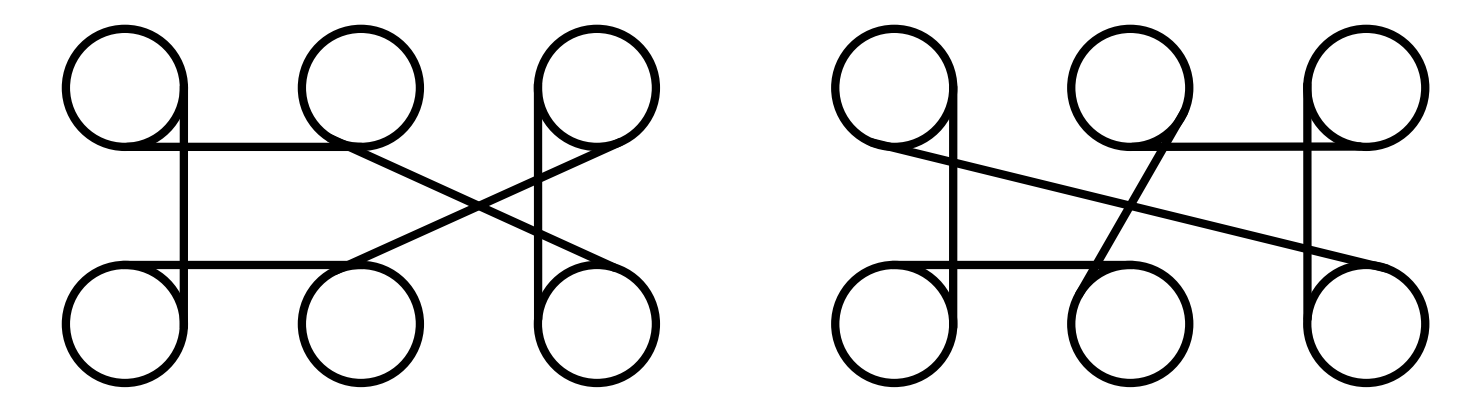
Potřebujeme spočítat délku úhlopříčných cest. To jde jednoduše pomocí Pythagorovy věty. Pro kratší úhlopříčnou cestu platí, že vzdálenost mezi středy stromů je \(\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}\). Přepona trojúhelníků na obrázku je tedy \(\sqrt{2}\) a kratší odvěsnu lze dopočítat z obvodu kmene, \(r=0,05\),m. Délka cesty bude \(2\sqrt{2-0,05^2}\). V druhém případě je vzdálenost středů \(\sqrt{4^2+2^2}=2\sqrt{5}\), délka cesty je \(2\sqrt{5-0,05^2}\).
Celkový součet délek hran v prvním případě je \(4\cdot 2+4\sqrt{2-0,05^2}\approx13,653...\) a víme, že na obvodech není možné přičíst více než \(0.6\pi\),m, tedy celková délka nebude větší než \(\approx 15,538...\). V druhém případě máme součet délek hran \(5\cdot 2+2\sqrt{5-0,05^2}\approx14,471...\) a lze snadno odpozorovat, že na obvodech kmenů přičteme minimálně \(4\cdot \frac{3}{4}0,1\pi+2\cdot \frac{5}{8}0,1\pi\),m, takže celková délka bude více než \(\approx 15,806...\), což je více než v prvním případě. Volíme proto prvního kandidáta.
Pro přesnou délku cesty nám zbývá dopočítat části obvodů kmenů (všechny následující výpočty budou v metrech). U dvou levých kmenů jde o \(\frac{3}{4}\) obvodu, tedy \(\frac{3}{4}\cdot 0,1\pi=\frac{3}{40}\pi\).
Při výpočtu pro prostřední a pravé kmeny si pomůžeme následujícím obrázkem, kde je pouze horní střední a dolní pravý kmen a vyznačené úhly, co nás budou zajímat.

U prostředních kmenů pokrývá provázek úhel \(2\pi-\alpha\) a \(\alpha=\frac{\pi}{2}-\frac{\pi}{4}-\beta\), protože součet vnitřních úhlů trojúhelníku je \(\pi\). Úhel \(\beta\) dopočítáme díky výpočtům výše pomocí funkce arkus sinus: \(\beta=\arcsin(\frac{0,05}{\sqrt{2}})\). A proto \(\alpha=\frac{\pi}{4}-\arcsin(\frac{0,05}{\sqrt{2}})\) a obvod bude \(\frac{1}{2\pi}(2\pi-\frac{\pi}{4}+\arcsin(\frac{0,05}{\sqrt{2}}))\cdot 0,1\pi=\frac{1}{2\pi}(\frac{7}{4}\pi+\arcsin(\frac{0,05}{\sqrt{2}}))\cdot 0,1\pi\).
U pravých kmenů nás zajímá úhel \(2\pi-\frac{\pi}{2}-\alpha=\frac{5}{4}\pi+\arcsin(\frac{0,05}{\sqrt{2}})\) a máme obvod \(\frac{1}{2\pi}(\frac{5}{4}\pi+\arcsin(\frac{0,05}{\sqrt{2}}))\cdot 0,1\pi\).
Celkově za všech šest kmenů máme:
\[{2\cdot \frac{3}{40}\pi+2\cdot \frac{1}{2\pi}(\frac{7}{4}\pi+\arcsin(\frac{0,05}{\sqrt{2}}))\cdot 0,1\pi+2\cdot \frac{1}{2\pi}(\frac{5}{4}\pi+\arcsin(\frac{0,05}{\sqrt{2}}))\cdot 0,1\pi}=\] \[=\frac{3}{20}\pi+\frac{1}{10}[\frac{7}{4}\pi+\arcsin(\frac{0,05}{\sqrt{2}})+\frac{5}{4}\pi+\arcsin(\frac{0,05}{\sqrt{2}})]=\] \[=\frac{3}{20}\pi+\frac{3}{10}\pi+\frac{1}{5}\arcsin(\frac{0,05}{\sqrt{2}})=\frac{9}{20}\pi+\frac{1}{5}\arcsin(\frac{0,05}{\sqrt{2}})\].
Nyní už snadno dopočítáme celkovou délku provázku: \[4\cdot 2+4\sqrt{2-0,05^2}+\frac{9}{20}\pi+\frac{1}{5}\arcsin(\frac{0,05}{\sqrt{2}})\approx15,07410685\doteq15,07411.\]