| Časový rozestup 40 s |
Zadání XVII. ročníku
2. sada
Sada 2
Konec odevzdávání: 24. listopadu 2025 18:00
16. Úhlová úloha:
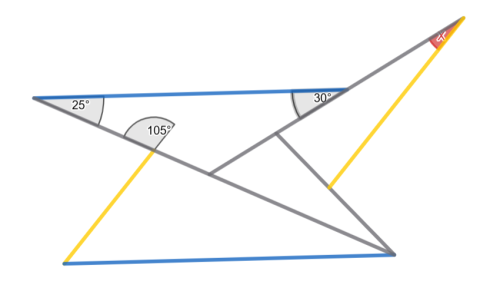
Jaká je velikost červeného úhlu \(x\)? (Víte, že vyznačené úhly jsou zleva 25°, 105°, 30° a žluté a modré úsečky jsou rovnoběžné. Zadejte ve stupních.)
Řešení
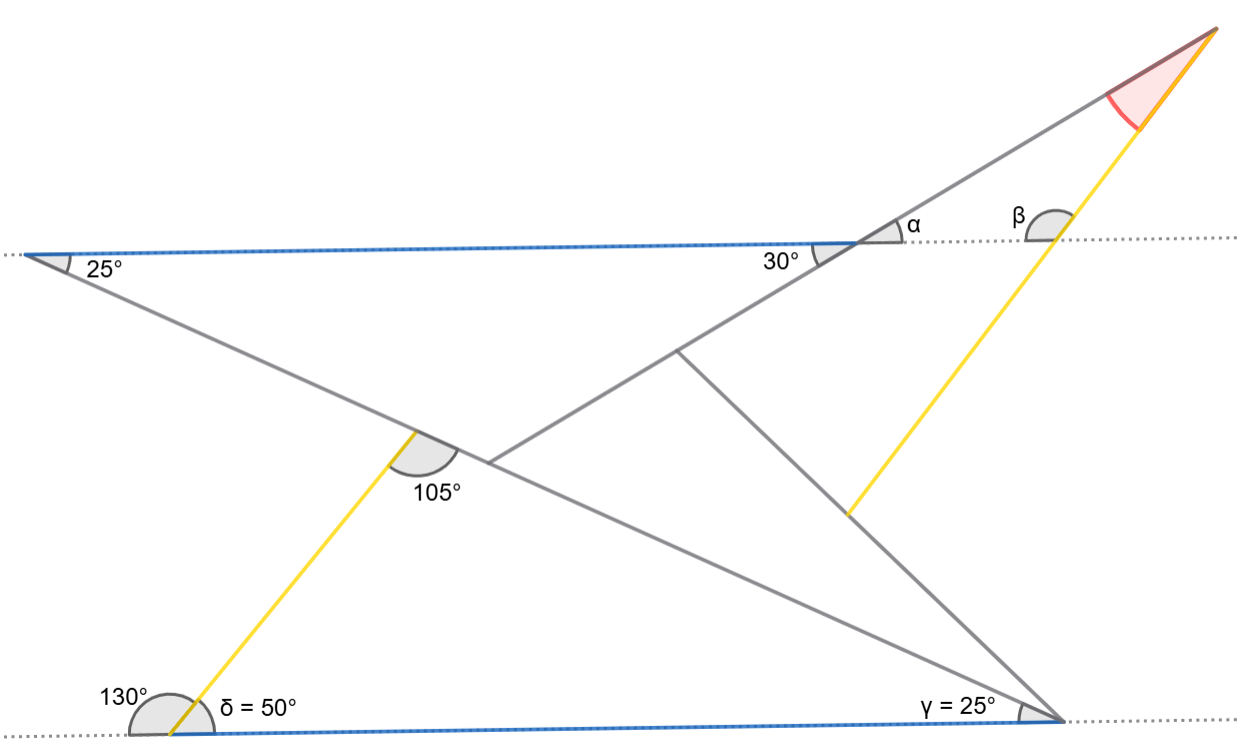
Jako první krok si prodloužíme modré rovnoběžky. Dále, čeho si můžeme hned všimnout je, že \(\alpha=30^\circ\), protože je to vrcholový úhel s úhlem ze zadání. Z vlastností rovnoběžek pak dostáváme \(\gamma=25^\circ\) a z vlastnosti trojúhelníků, že součet jejich vnitřních úhlů je vždy \(180^\circ\), vidíme, že \(\delta=(180-105-25)^\circ=50^\circ\). Opět z vlastnosti rovnoběžek ale dostáváme, že \(\beta\) a vedlejší úhel úhlu \(\delta\) mají stejnou velikost, tzn. \(\beta=(180-50)^\circ=130^\circ\). Celkem tedy máme: \[x=(180-\alpha-\beta)^\circ=(180-30-130)^\circ=20^\circ\]
17. Brkořeka:
Oskar, Lukáš, Ráďa a Tonda se potřebují dostat z jednoho břehu řeky na druhý. Bohužel ale mají pouze jedny siamské brkoplavky, do kterých se najednou vejdou maximálně dva. Najednou tedy mohou řeku přeplavávat maximálně dva, a to pouze pokud na jejich břehu jsou plavky. Oskar řeku přeplave za \(1\) minutu, Lukáš za \(2\) minuty, Ráďa za \(5\) minut a Tonda za \(10\). Pokud plavou dva spolu, budou plavat rychlostí toho pomalejšího. Za kolik minut můžou být nejdříve všichni na druhém břehu?
Řešení
Klíčem k minimalizaci celkového času je zajistit, aby nejpomalejší (Ráďa a Tonda) přeplavali řeku společně, a aby zpět plavali vždy ti nejrychlejší (Oskar a Lukáš).
| Krok | Pasažéři | Čas | Startovní břeh | Cílový břeh | Kumulativní čas |
|---|---|---|---|---|---|
| 1 | O + L (přes) | \(2\) | R, T | O, L | \(2\) |
| 2 | O (zpět) | \(1\) | O, R, T | L | \(2 + 1 = 3\) |
| 3 | R + T (přes) | \(10\) | O | L, R, T | \(3 + 10 = 13\) |
| 4 | L (zpět) | \(2\) | O, L | R, T | \(13 + 2 = 15\) |
| 5 | O + L (přes) | \(2\) | \(\emptyset\) | O, L, R, T | \(15 + 2 = 17\) |
Všichni mohou být nejdříve na druhém břehu za \(\mathbf{17}\) minut.
18. Za sedmero horami:
Libovolné přirozené číslo můžeme redukovat pomocí jeho ciferného součtu až na jednociferné číslo. Např. číslo \(987\) zredukujeme na \(9+8+7 = 24\) a to zredukujeme na \(2+4 = 6\). Redukce čísla \(987\) je tedy číslice \(6\). Kolik existuje čísel do \(999\), která se zredukují na číslici \(7\)?
Řešení
Jak je známo, ciferný součet zachovává zbytek po dělení devíti (neboť \(10^n\equiv 1 \mod 9\)). Tedy nutně i opakovaný ciferný součet. Proto se číslo zredukuje na \(7\) právě tehdy, když dává zbytek \(7\) po dělení devíti. Takových čísel je v rozmezí do \(999\) právě \(111\).
19. Procházení:
Máme kvadratický polynom, který má v bodech \(1,2,3\) následující funkční hodnoty: \(f(1)=18,\)$ f(2)=38, f(3)=64$. Najděte tento polynom a jako řešení zapište absolutní hodnoty jeho koeficientů za sebe, např. \(1213\) pro \(x^2 - 21x + 3\).
Řešení
Kvadratické polynomy jsou tvaru \(f(x) = ax^2 + bx + c\). Tuto úlohu lze vyřešit mnoha způsoby, například tipováním, dokud to nezačne sedět, nebo vyřešením následující soustavy lineárních rovnic: \[\begin{aligned} f(1) = a + b + c &= 18 \\ f(2) = 4a + 2b + c &= 38 \\ f(3) = 9a + 3b + c &= 64 \\ \\ 3a + b &= 20 \\ 8a + 2b &= 46 \\ \\ 2a &= 6 \Rightarrow a = 3 \\ 3a + b = 9 + b &= 20 \Rightarrow b = 11 \\ a + b + c = 14 + c &= 18 \Rightarrow c = 4 \\\end{aligned}\] Takže \(f(x) = 3x^2 + 11x + 4\), a výsledek je \(3114\).
20. Svanička:
Anička má vždy po učení matematiky velký hlad, proto se rozhodla všem \(30\) žákům sníst svačinu. Aby to bylo zajímavé, žáky nechala sednout do kružnice, rovnoměrně daleko od sebe. Aniččino svačení probíhalo následovně: sní někomu svačinu, jde po směru hodinových ručiček. Počítá si, okolo kolika žáků, kteří ještě mají svačinu, prošla. Jakmile narazí na sedmého takového žáka, sní mu svačinu a dále pokračuje stejným způsobem. (Jakmile tedy zbyde poslední žák, chuděra Anička musí obejít \(7\) kol, než mu bude moci sníst svačinu.) Skončí, když sní poslední svačinu. Kolik celkem ujde úhlových stupňů kolem kružnice?
Řešení
Bohužel nám nezbyde nic jiného než projít si Aniččinu cestu a postupně škrtat studenty se snězenou svačinou. Doporučujeme si označit studenty čísly \(1\) až \(30\). Dopočítáme úhel mezi studenty jako \(\alpha=\frac{360^\circ}{30}=12^\circ\). Vytvoříme si hezký nákres a pustíme se do díla. Takto vypadá situace po prvním obejití kruhu:
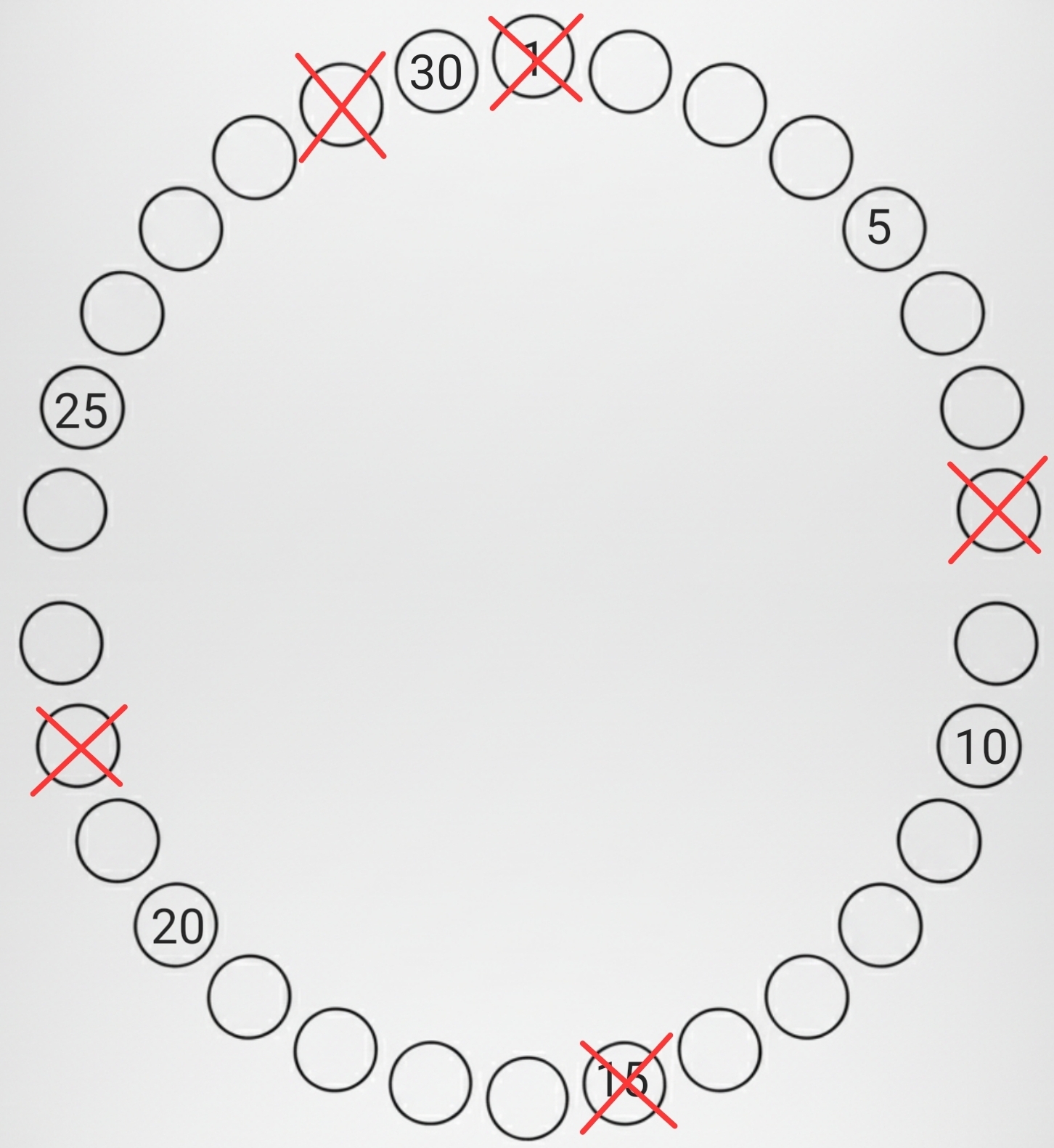
A pro pořádek uvádíme i tabulku s čísly studentů, jimž byla v daném kole snězena svačina:
| Kolo | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Snězeno | 1,8,15,22,29 | 7,16,24 | 3,12,21 | 2,13,25 | 6,19 | 4,18 | 5,23 |
| Kolo | 8 | 9 | 10 | 11 | 13 | 15 | 17 | 20 | 26 |
|---|---|---|---|---|---|---|---|---|---|
| Snězeno | 11,30 | 27 | 26 | 28 | 10 | 20 | 9 | 14 | 17 |
Skončili jsme ve \(26.\) kole u sedmnáctého studenta, celkem tedy Anička obešla \[25\cdot360^\circ+16\cdot\alpha=9192^\circ\]
21. Ráďa s Leou permutují:
Na stole jsou v řadě papírky s čísly 1 až 12 seřazené vzestupně. Prvně přijde Lea a zamíchá je opět do řady tak, že číslo, které bylo na daném místě původně, má stejný zbytek po dělení třemi jako nové číslo. Potom přijde Ráďa a opět čísla zamíchá, tentokrát tak, že nová čísla mají stejnou paritu jako ta, která byla na daném místě po Leině zamíchání. Kolik je možností, jak řada čísel vypadá na konci?
Řešení
Podívejme se, co se může stát s čísly \(1, 4, 7, 10\). Všechna mají stejný zbytek po dělení třemi, a tak při Leině zamíchání dojde k nějaké jejich permutaci. Dvě z nich jsou sudá a dvě lichá, což se zachová i při Rádině zamíchání. Na konci tedy na těchto místech musí být čtveřice čísel, z nichž dvě jsou sudá a dvě lichá. To samé platí i pro čtveřice čísel se zbytky \(2\) a \(0\).
Dále vysvětlíme, že každé takové zamíchání, které zachovává počty sudých a lichých čísel ve čtveřicích, můžeme získat. Každé dvojici zbytků po dělení třemi a dvěma odpovídají dvě čísla. Známe-li počáteční pořadí a konečné pořadí papírků, dostáváme na každém místě dvě možnosti, jak mohlo vypadat prostřední zamíchání. Když bude konečné pořadí splňovat naši podmínku, budou každé dvojici možných čísel v prostředním zamíchání odpovídat dvě pozice. Stačí tedy tato dvě čísla na daná místa nějak přiřadit a dostáváme dvojici permutací, která vyhovuje. (Tato volba znamená, že při znalosti začátečního a konečného pořadí existuje více možností – konkrétně \(2^6\) – dvojic permutací Ley a Rádi.)
Nakonec nám stačí rozhodnout, kolik koncových pořadí vyhovuje. Vyberme nejprve dvě lichá a dvě sudá čísla pro pozice odpovídající papírkům \(1, 4, 7, 10\) a ta libovolně seřaďme. Takto dostáváme \({6 \choose 2}^2 \cdot 4!\) možností. Analogicky pro druhou čtveřici už vybíráme pouze ze čtyř sudých a lichých čísel, máme tedy \({4 \choose 2}^2 \cdot 4!\) možností a pro poslední čtveřici už není co vybírat a zbývá \(4!\) možností.
Dohromady tedy máme \({6 \choose 2}^2 \cdot 4!\cdot {4 \choose 2}^2 \cdot 4!\cdot 4! = 111 974 400\) možností. Poznamenejme, že pokud k výsledku můžeme dojít i v tomto tvaru: \(\frac{4!^3\cdot 6!^2}{2^6}\), kde v čitateli je součin možností pro obě zamíchání a ve jmenovateli počet dvojic zamíchání, která vedou ke stejné řadě papírků na konci.
22. Palilap:
Kolik je sedmiciferných palindromů takových, že po vynásobení jedenácti už nebudou palindromem?
Řešení
Sedmiciferný palindrom si pomocí proměnných můžeme zapsat jako {ABCDCBA}. Z tohoto zápisu můžeme jednoduše spočítat počet všech sedmiciferných palindromů: za A můžeme dosadit 9 cifer (1-9) a za B, C a D 10 cifer (0-9), tedy máme celkem \(9\cdot 10 \cdot 10\cdot 10=9000\) palindromů. Nyní můžeme spočítat kolik palindromů po vynásobení 11 stále palindromem je a řešení poté dopočítat.
| A | B | C | D | C | B | A | |
| \(\cdot 11\) | |||||||
| A | B | C | D | C | B | A | |
| A | B | C | D | C | B | A | |
| A | A+B | B+C | C+D | C+D | B+C | A+B | A |
Aby byl součin palindromem, musí platit následující nerovnosti, jinak by přenášení jedničky narušilo symetrii cifer (např. kdyby \(a+b\geq 10\), první cifra by už neodpovídala poslední):
\(a+b<10\)
\(b+c<10\)
\(c+d<10\)
Počet palindromů zjistíme přes fixaci dvojice \((b,c)\) a dopočítáním počtu možností zvolení \(a,d\). Vzor chování ukazuje tabulka pro \(b=0,1\).
| (b,c) | a | d | možností |
|---|---|---|---|
| (0,0) | 9 | 10 | 90 |
| (0,1) | 9 | 9 | 81 |
| \(\vdots\) | \(\vdots\) | ||
| (0,9) | 9 | 1 | 9 |
| (1,0) | 8 | 10 | 80 |
| (1,1) | 8 | 9 | 72 |
| \(\vdots\) | \(\vdots\) | ||
| (1,8) | 8 | 2 | 16 |
Počet možností pro dané \(b\) můžeme na základě pozorování z tabulky zapsat jako sumu: \(b\sim \sum_{c=0}^{9-b}(9-b)\cdot (10-c)\). Celkový počet palindromů s požadovanou vlastností je \(\sum_{b=0}^{8}{\sum_{c=0}^{9-b}(9-b)\cdot (10-c)}\), pro \(b=9\) není žádná možnost pro \(a\), proto suma končí 8. Počet palindromů, které po vynásobení 11 zůstanou palindromem je \(495+432+364+294+225+160+102+54+19=2145\). Odpověď, kolik palindromů nebude po vynásobení 11 palindromem, je \(9000-2145=6855\).
23. Volejbalový turnaj:
Štěpán hrál volejbal a za stavu \(24:23\) (pro něj) začalo pršet. Protože už nebyl čas set dohrát, týmy se dohodly, že si o každý další bod hodí mincí. Soupeř ale vytáhl falešnou minci a bude mu padat rub s pravděpodobnosti \(\frac{2}{3}\). (Štěpán získá bod, pokud na minci padne líc.) S jakou pravděpodobností Štěpán set vyhraje, pokud se hraje do \(25\) bodů, přičemž výsledný stav musí být o dva?
Řešení
Označme A pravděpodobnost že Štěpánův tým vyhraje, když je teď ve stavu 24:23 (tedy A je řešení úlohy). Dále označme B pravděpodobnost, že vyhraje poté, co se dostane do stavu 24:24. Nyní tedy poprvé házejí mincí a Štěpán s pravděpodobností \(\frac{1}{3}\) ihned vyhraje a s pravděpodobností \(\frac{2}{3}\) se dostane do stavu 24:24, kde má pravděpodobnost na výhru B, tedy
\[A = \frac{1}{3} + \frac{2}{3}B.\]
Nyní je potřeba si uvědomit, že pro všechna skore vyšší než 23:23 pravděpodobnost výhry nezávisí na přesném skore, ale pouze na rozdílu bodů, např. pokud je skore shodne je potřeba pro výhru dát v následujících dvou hodech dva body, nebo ve čtyřech dát tři body atd., nezáleží jestli je to 25:25, nebo 27:27. Podobně v našem případe je pravděpodobnost pro 25:24 stejná jako pro 24:23, tedy A. Dostáváme rovnici
\[B = \frac{1}{3} A + \frac{2}{3}C,\]
kde C je pravděpodobnost výhry za stavu 24:25. Tu můžeme podobně jako první rovnici vyjádřit pomocí B jako
\[C = \frac{2}{3}0 + \frac{1}{3}B = \frac{1}{3}B.\]
Soustavu tří rovnic vyřešíme například dosazením do druhé rovnice
\[B = \frac{1}{3} (\frac{1}{3} + \frac{2}{3}B) + \frac{2}{3}\frac{1}{3}B.\]
24. Právnické bezpráví:
Kačka skládá zkoušku z pracovního práva. Čeká ji test o \(10\) otázkách s třemi odpověďmi, kde \(0-3\) odpovědí je správně. Aby zkoušku zvládla, musí mít alespoň \(7\) otázek dobře, přičemž u každé odpovědi si je jistá jen na \(90~\%\). S jakou pravděpodobností úspěšně zvládne zkoušku?
Řešení
Aby Kačka správně odpověděla na jednu otázku, musí správně vyplnit každou z odpovědí dané otázky (všechny i žádná odpověď mohou být správně). Pravděpodobnost, že Kačka odpoví na jakoukoliv otázku správně je tedy \(0.9^3\). Nyní potřebujeme zjistit, s jakou pravděpodobností bude správných otázek alespoň \(7\). Můžeme si uvědomit, že hledáme počet úspěchů z \(10\) pokusů s tím, že každý úspěch má pravděpodobnost \(0.9^3\). Toto je přesně binomické rozdělení pomocí kterého jsme schopni najít pravděpodobnost přesného počtu úspěšných otázek.
Jelikož je úspěšných otázek maximálně \(10\), tak abychom uvažovali všechny možnosti, kdy máme alespoň \(7\) otázek správně, musíme najít pravděpodobnost pro \(7,\: 8,\: 9,\: 10\) úspěšných otázek. Pravděpodobnost \(7\) úspěšných otázek je \({10 \choose 7} \cdot (0.9^3)^7 \cdot (1-0.9^3)^3\). Pro \(8\) úspěšných otázek následně \({10 \choose 8} \cdot (0.9^3)^8 \cdot (1-0.9^3)^2\), pro \(9\) je pravděpodobnost \({10 \choose 9} \cdot (0.9^3)^9 \cdot (1-0.9^3)^1\) a pro \(10\) je pravděpodobnost \({10 \choose 10} \cdot (0.9^3)^{10} \cdot (1-0.9^3)^0\).
Pokud všechny tyto pravděpodobnosti sečteme, máme výsledek \(0.72492\).
25. Devytelé:
Dělitele \(n>1\) čísla \(a\) nazveme Devytelem, pokud \((n+1)\mid a\). Najděte nejmenší číslo \(k\) takové, že \(k\) má právě \(4\) Devytele a \(2k\) má právě \(7\) Devytelů.
Řešení
Uvědomíme si, že číslo \(n\) je Devytelem čísla \(k\) právě tehdy, když \(n(n+1)\mid k\). Tedy zkoumáme dělitelnost čísly \(6,12,20,30,42,56,72\dots\) Dále lze řešit dvěma způsoby:
Zkoušením, a sice vypsáním nejmenších společných násobků (alespoň) čtveřic čísel typu \(n(n+1)\). Dostaneme posloupnost kandidátů \(60,120,168,180,210,240,300,332,360,420,\dots\) Vyškrtneme ty členy, které mají více než čtyři Devytele a hledáme ty, jejichž dvojnásobek má \(7\) Devytelů. Nejmenší takové číslo je \(k=210\).
Všimneme si, že všechna z čísel typu \(n(n+1)\) jsou dělitelná dvěma, zhruba polovina čtyřmi a jen málo osmi. Pokud by tedy platilo \(4\mid k\), číslo \(2k\) by mělo navíc ty Devytele, kteří jsou dělitelní osmi. Těch je málo, tedy by \(k\) muselo být velké. Přijmeme tedy předpoklad \(2\mid k, 4\nmid k\) a zkonstruujeme co nejmenší číslo mající \(4\) Devytele. Rychle dojdeme k \(k=2\cdot 3\cdot 5\cdot 7=210\)
26. Babička zabíjí slimáky na poli:
Babička má pole tvaru kruhu o poloměru \(1\) km. Pole však napadli slimáci. Babička vlastním tělem chránila pravidelný \(n\)-úhelník vepsaný kruhu. Pak se ale unavila a poslala místo sebe hlídat jejího vlčáka Štěpána, který hlídá pravidelný \(2n\)-úhelník vepsaný kruhu. Za předpokladu, že Štěpán uhlídá přibližně \(1,0094\times\) větší plochu než babička, určete \(n\in\mathbb{N}\).
Řešení
Vzorec pro obsah pravidelného \(n-\)úhelníku (vepsaného kružnici) je \[S_n=\frac{1}{2}nr^2 \sin\frac{2\pi}{n}\] Vyjádříme stejným způsobem obsah \(2n-\)úhelníku, dosadíme \(r=1\) a upravujeme rovnici \[1,0094 = \frac{S_{2n}}{S_n} = \frac{\frac{1}{2}2n \sin\frac{2\pi}{2n}}{\frac{1}{2}n \sin\frac{2\pi}{n}} = \frac{n\sin\frac{\pi}{n}}{\frac{1}{2}n \sin\frac{2\pi}{n}} = \frac{n\sin\frac{\pi}{n}}{\frac{1}{2}n\cdot2\sin\frac{\pi}{n}\cos\frac{\pi}{n}} = \frac{1}{\cos\frac{\pi}{n}}\] kde čtvrté \(=\) je využití vzorce \(\sin2\alpha=2\sin\alpha\cos\alpha\) ve jmenovateli. Z takto zjednodušeného vzorce již snadno dopočítáme \(n\) jakožto \[n=\frac{\pi}{\arccos\frac{1}{1,0094}}=23,00196\dots\approx23\]
27. Foodcourt:
Ve foodcourtu jsou tři fastfoody: TerkaTaco, LeaLívance a PeťaPho. Uvažujme zákazníky, kteří chodí do foodcourtu každý den a vybírají si právě jeden z fastfoodů. Pokud zákazník jeden den navštíví PeťaPho, další den jej navštíví s \(90\%\) pravděpodobností. Pro LeaLívance a TerkaTaco je tato pravděpodobnost \(80~\%\). Pokud se zákazník rozhodne změnit fastfood, vybere si náhodně mezi zbývajícími dvěma, a to se stejnou pravděpodobností. Najděte takové rozdělení zákazníků mezi obchody, při kterém bude podíl zákazníků navštěvující jednotlivé obchody konstantní, tj. pokud v jeden den navštěvovalo fastfoody \((p_1, p_2, p_3)~\%\) zákazníků, další den bude fastfoody opět navštěvovat \((p_1, p_2, p_3)~\%\) zákazníků. Jako odpověď zadejte podíl zákazníků takto navštěvujících TerkaTaco.
Řešení
Označme stejně jako v zadání \((p_1, p_2, p_3)\) rozložení zákazníků mezi jednotlivé fastfoody (v pořadí TerkaTaco, LeaLívance, PeťaPho) v nějaký den. Podle zadání bude další den rozložení následující: \[(0,8 p_1 + 0,1 p_2 + 0,05 p_3; 0,8 p_2 + 0,1 p_1 + 0,05 p_3; 0,9 p_3+0,1 p_1 + 0,1 p_2).\] Aby byly poměry návštěvníků konstantní, řešíme soustavu rovnic: \[p_1 = 0,8 p_1 + 0,1 p_2 + 0,05 p_3,\]\[p_2 = 0,8 p_2 + 0,1 p_1 + 0,05 p_3,\]\[p_3 = 0,9 p_3+0,1 p_1 + 0,1 p_2.\]
Jejím jediným řešením takovým, že \(p_1 + p_2 + p_3 =1\) (tedy součet zákazníků dá \(100 \%\)), je trojice \((\frac{1}{4}, \frac{1}{4}, \frac{1}{2})\). TerkaTaco tedy navštěvuje \(\frac{1}{4}\) zákazníků.
28. Olympiádní matematika:
Olympijská vlajka se skládá z pěti kruhů se středy v rovnostranných trojúhelnících o straně délky \(100\sqrt{3}\) cm, rozložených jako na obrázku. Poloměr kruhu je \(100\) cm. Spočítejte, jakou plochu zabírají kruhy (zaokrouhlete na setiny).
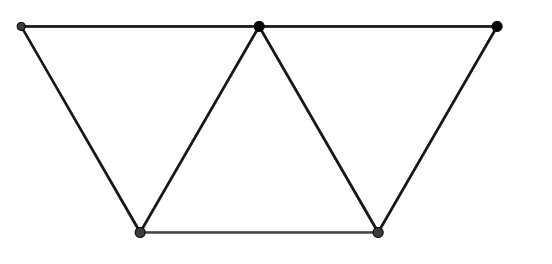
Řešení
Prvním klíčovým krokem bude nakreslit si správný obrázek. Trojúhelníky jsou rovnostranné se stranou délky \(100\sqrt{3}\). Jejich výšky tedy budou o rozměrech \[\sqrt{10000\cdot3 - 2500\cdot3} = \sqrt{7500\cdot3} = 150 cm.\] Současně poloměry kružnic jsou rovny \(100\) cm, což znamená, že se tři kružnice se středy ve vrcholech jednoho trojúhelníku protnou v ortocentru, nebo také těžišti trojúhelníku. Jsme tedy nyní už připraveni si nakreslit obrázek.
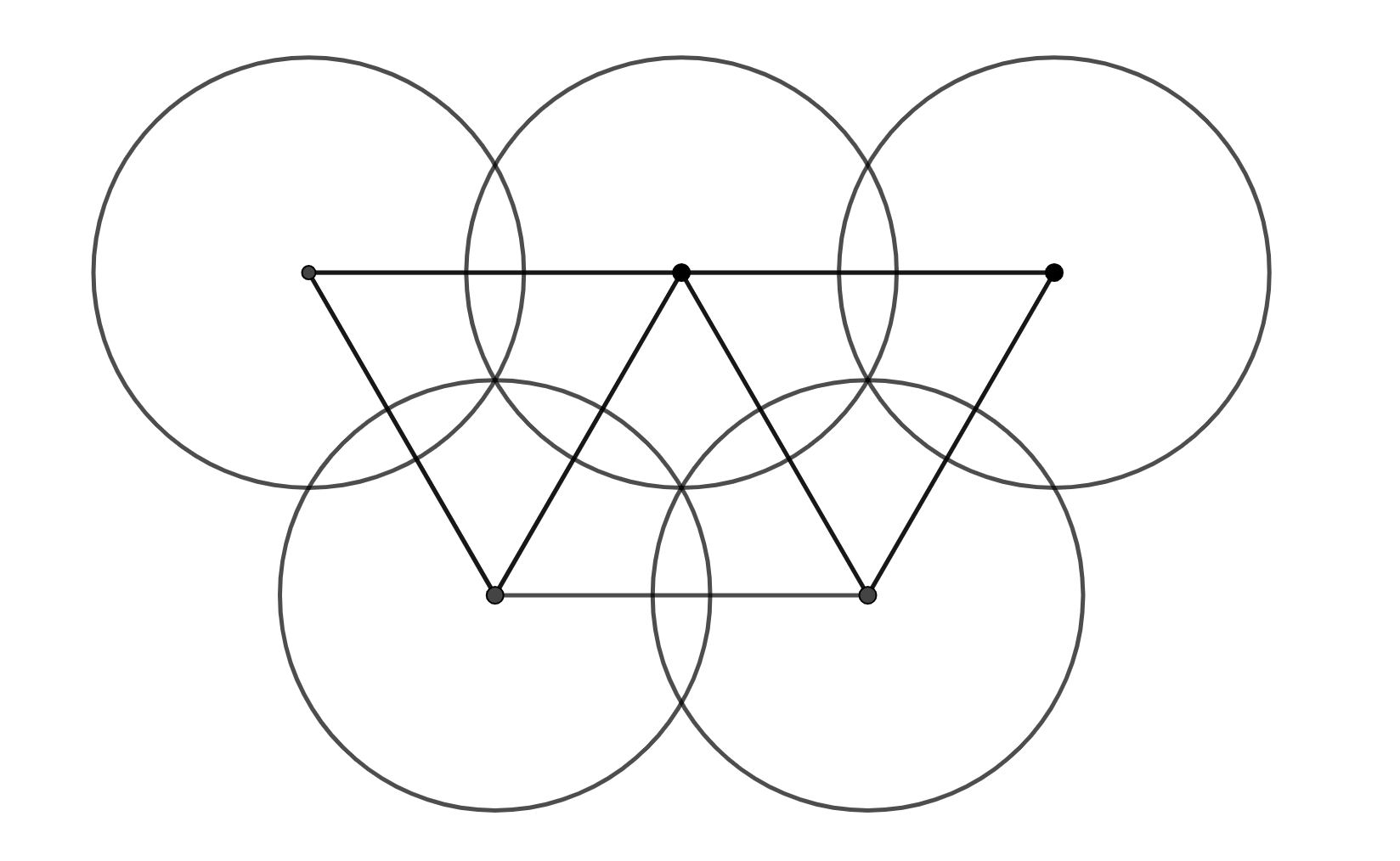
Vzhledem k tomu, že se kružnice protínají v jednom bodě, znamená to, že se vždy překrývá pouze dvojice kruhů v určité kruhové výseči. Pojďme spočítat její obsah.
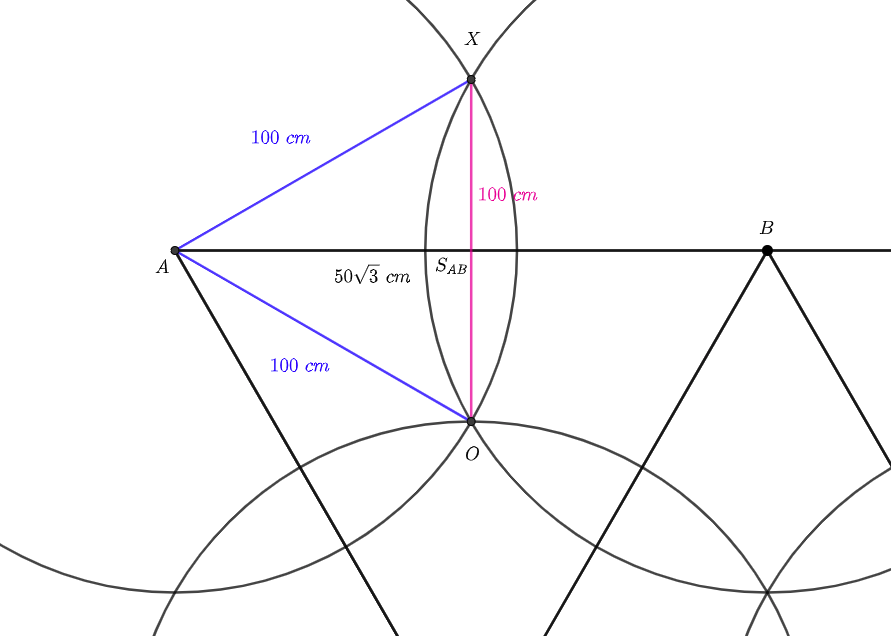
\(AS\) bude kolmá na \(OX\), a proto \[|\angle S_{AB}AO| = 30^\circ ,\] z čehož získáme, že \(AOX\) je rovnostranný trojúhelník se stranou 100 cm. Obsah trojúhelníka proto spočítáme jako \(100 \cdot 50\sqrt{3} / 2\) a obsah kruhové výseče \(OAX\) bude roven \(\pi 100^2 / 6\). Obsah dvou kruhových úsečí, ve kterých se dvě kružnice protínají proto bude \[\begin{aligned} 2 \cdot \frac{10000\pi}{6} - 2\cdot \frac{5000\sqrt{3}}{2}\end{aligned}\]
Celková plocha, kterou kruhy zabírají proto bude plocha všech kruhů \(5 \cdot \pi 100^2 \cdot 3\) bez sedmi dvojúsečí tj. \[\begin{aligned} 5 \cdot \pi 100^2 \cdot 3 - 14 \cdot \frac{10000\pi}{6} + 14 \cdot \frac{5000\sqrt{3}}{2} = 144397.58\end{aligned}\]
29. Střelec Petr:
Petr hrál s taťkou v obýváku šachy a ztratili bílého střelce. Pak půjčil šachy malému Davidovi a věděl, že s pravděpodobností \(0.5\) Davídek ztratí jednu další figurku (všechny se stejnou pravděpodobností). Večer Davídek šachy uklidil a druhý den Petr začal hledat a první figurka, kterou našel, byla bílý střelec. (Pokud by byly ztracené dvě figurky, byla stejná pravděpodobnost, že najde první jednu nebo druhou.) V tu chvíli se Petr zaradoval, protože tato skutečnost částečně napovídá, že Davídek figurku neztratil. Jaká je pravděpodobnost, že když Petr teď otevře krabici a doplní střelce, bude mít kompletní sadu šachů?
Řešení
Jedná se o pravděpodobnostní problém, tak si rozepíšeme všechny možné jevy. Víme, že už byl ztracen jeden bílý střelec. Dále:
Davídek nic neztratí. \(P(A)=\frac{1}{2}\)
Davídek ztratí bílého střelce. Pravděpodobnost, že figurku ztratí, je jedna polovina a tu vynásobíme pravděpodobností, že ztracená figurka je bílý střelec, tedy jedna figurka ze zbývajících 31. \(P(B)=\frac{1}{2}\cdot \frac{1}{31}\)
Davídek ztratí figurku různou od bílého střelce. Pravděpodobnost ztracení vynásobenou pravděpodobnostní určující typ figurky musíme vynásobit ještě jednou polovinou, jelikož víme, že Petr druhý den našel bílého střelce (na to měl pravděpodobnost jedna polovina). \(P(C)=\frac{1}{2}\cdot \frac{30}{31} \cdot \frac{1}{2}\).
Tedy celková pravděpodobnost, že naše situace nastane, je \(\frac{1}{2}+\frac{1}{2}\cdot \frac{1}{31}+\frac{1}{2}\cdot \frac{30}{31} \cdot \frac{1}{2}=\frac{47}{62}\). Nás zajímá pravděpodobnost, že sada je kompletní, tedy v jak velké části naší situace je kompletní, a to odpovídá jevu, že Davídek nic neztratí. \(P=\frac{P(A)}{P(A)+P(B)+P(C)}=\frac{\frac{1}{2}}{\frac{47}{62}}=\frac{62}{2\cdot 47}=\frac{31}{47}\).
30. Pátá právě se odmocnila:
Devy si chce přidat do salátu číslo \(d = \sqrt[7]{\sqrt{5}+\sqrt{5+\sqrt{5}}}\), aby si ho ale mohl přidat, potřebuje vědět, jestli je to kořenová zelenina. Najděte normovaný (koeficient u vedoucího členu - členu s nejvyšší mocninou - je jedna) polynom (\(28.\) stupně) s celočíselnými koeficienty takový, že číslo \(d\) je jeho kořenem. Jako odpověď zadejte součet všech jeho koeficientů.
Řešení
Ze zadání víme, že platí \[\begin{aligned} d = \sqrt[7]{\sqrt{5}+\sqrt{5+\sqrt{5}}}\end{aligned}\] Pojďme si hrát s touto rovnicí, abychom se zbavili odmocnin. \[\begin{aligned} d &= \sqrt[7]{\sqrt{5}+\sqrt{5+\sqrt{5}}} \\ d^7 &= \sqrt{5}+\sqrt{5+\sqrt{5}} \\ d^7 - \sqrt{5} &= \sqrt{5+\sqrt{5}} \\ d^{14} - 2\sqrt{5}d^7 + 5 &= 5+\sqrt{5} \\ d^{14} - 2\sqrt{5}d^7 &= \sqrt{5} \\ d^{14} &= 2\sqrt{5}d^7 + \sqrt{5} \\ d^{28} &= 20d^{14} + 20d^7 + 5 \\ d^{28} - 20d^{14} - 20d^7 - 5 &= 0 \\\end{aligned}\]
Tím, že jsme původní rovnici pro kořen umocňovali, tak jsme získali polynom \(P(x) = x^{28} - 20x^{14} - 20x^7 - 5\), který má celočíselné koeficienty a současně \(d\) za kořen. Zadat jako odpověď pak musíme \(1-20-20-5 = -44\).