| Časový rozestup 40 s |
Zadání XVI. ročníku
2. sada
Sada 2
Konec odevzdávání: 27. listopadu 2024 18:00
16. Polynom se vrací!:
Anička se na přednášce naučila o zajímavém polynomu. Na zkoušce ovšem zjistila, že ho zapomněla. Zapamatovala si pouze, že byl tvaru \(x^3 + ax^2 + b\), a že jeho kořeny tvořily aritmetickou posloupnost. Pomozte jí určit \(\frac{b}{a^3}\).
Řešení
Použijeme legendární vlastnost kořenů polynomu, a to konkrétně Vietovy vztahy. Víme, že polynom, má tři reálné kořeny. Nazveme je \(x_1, x_2, x_3\) tak, že \(x_1 < x_2 < x_3\). Pak určitě platí: \[\begin{aligned} x^3 + ax^2 + b &= (x - x_1)(x - x_2)(x - x_3) \\ &= x^3 - (x_1 + x_2 + x_3)x^2 + (x_1x_2 + x_2x_3 + x_3x_1)x - x_1x_2x_3 \end{aligned}\] A jelikož rovné polynomy musí mít rovné všechny koeficienty, tak máme: \[\begin{aligned} -a &= x_1 + x_2 + x_3 \\ 0 &= x_1x_2 + x_2x_3 + x_3x_1 \\ -b &= x_1x_2x_3 \end{aligned}\] Dále ještě víme, že kořeny tvoří aritmetickou posloupnost. Pak existují \(m, d\) takové, že: \[\begin{aligned} x_1 &= m - d \\ x_2 &= m \\ x_3 &= m + d \end{aligned}\] Nyní jsou to již jen algebraické úpravy: \[\begin{aligned} -a &= x_1 + x_2 + x_3 = m - d + m + m + d = 3m \\ 0 &= x_1x_2 + x_2x_3 + x_3x_1 = (m-d)m + m(m+d) + (m-d)(m+d) = 3m^2 - d^2 \\ -b &= x_1x_2x_3 = (m - d)m(m + d) = m^3 - md^2 \\ \end{aligned}\] Z první rovnice máme \(m = \frac{-a}{3}\). Z druhé máme: [ d^2 = 3m^2 = 3 = \ ] Ze třetí se vše dourčí: \[\begin{gathered} -b = m^3 - md^2 = \frac{-a^3}{27} - \frac{-a}{3} \cdot \frac{a^2}{3} = \frac{2a^3}{27} \\ \frac{b}{a^3} = -\frac{2}{27} \end{gathered}\]
Výsledek je tudíž \(-\frac{2}{27}\).
17. Kolečka:
Uvažujme tři kružnice se stejným poloměrem \(r=2\) takové, že každé dvě mají vnější dotyk. Určete obsah oblasti mezi těmito kružnicemi
Řešení
Zadání si zakreslíme do obrázku.

Z něj je zřejmé, že \(\triangle ABC\) je rovnostranný s délkou strany \(4 cm\) a body dotyku \(E, F, G\) jsou jeho střední příčky. \(\triangle ABC\) tak dělí na \(4\) shodné trojúhelníky, které oproti němu mají čtvrtinový obsah a jsou mu podobné s koeficientem podobnosti \(2\).\
Vidíme, že obsah každé ze zelených oblastí je rozdíl obsahu kruhové výseče, určené stranami \(\triangle ABC\), a jednoho z těchto menších rovnostranných trojúhelníků. Dále oranžová oblast je rovna obsahu \(\triangle DEF\) zmenšenému o trojnásobek obsahu zelené oblasti.\
Středový úhel kruhové výseče je \(60^{\circ}\), jelikož splývá s \(\angle BCA\), a tudíž obsah výseče bude šestina obsahu kružnice se středem v \(C\), tedy \(\frac{\pi \cdot 2^2}{6} = \frac{2}{3}\pi\).\
Dále si spočítáme obsah např. \(\triangle ADF\). \(|AD| = 2\) a výška na tuto stranu je z Pythagorovy věty \(\sqrt{2^2 - 1^2} = \sqrt{3}\). Obsah zelené oblasti tak můžeme vyjádřit jako \(\frac{2}{3}\pi - \sqrt{3}\).\
Na závěr pak znovu využijeme vypočítaný obsah \(\triangle ADF\) a zelené oblasti a vypočítáme obsah oranžové oblasti jako:
\(\sqrt{3} - 3 \cdot (\frac{2}{3}\pi - \sqrt{3}) = 4\sqrt{3} - 2\pi \approx 0.64502\) \({cm}^2\).
18. Neklesající posloupnost:
Kolik existuje maximálně čtyřciferných čísel takových, že jejich cifry tvoří neklesající posloupnost, jejich ciferný součet je nejvýše \(13\) a dávají zbytek \(1\) po dělení \(5\)?
Řešení
Dané číslo musí mít na pozici jednotek \(1\) nebo \(6\), aby platilo, že po dělení pěti dává zbytek \(1\). V následující tabulce jsou vypsána čísla s neklesajícími ciframi (tj. buď jsou stejné, nebo postupně rostou) a jejich ciferné součty. Pokud \(CS \geq 13\), dané číslo nemá smysl zvětšovat a na dalším řádku se pokračuje zavedeným principem vypisování / novou číslicí. Např. \(CS(2236)=13 => 2336\) neřešíme.  Celkem existuje 34 vyhovujících čísel.
Celkem existuje 34 vyhovujících čísel.
19. Hrací automat:
Lukáš šel do kasína a sedl si k hracímu automatu. Má deset žetonů. Po vhození prvního žetonu má pravděpodobnost na výhru \(1.5\) %. Když prohraje, může vhodit další žeton s tím, že pravděpodobnost na výhru je každé další kolo o \(1.5\) % vyšší; tedy první kolo \(1.5\) %, druhé kolo \(3\) %, třetí kolo \(4.5\) % a tak dále. Když vyhraje, vezme si výhru a odejde, jinak odejde po deseti pokusech bez výhry. Jaká je pravděpodobnost, že odejde s výhrou?
Řešení
Mohou nastat pouze dvě možnosti – buď Lukáš po nějakém počtu kol vyhraje, nebo ne. Pravděpodobnost, že se mu to podaří, spočítáme jako jedna mínus šance, že odejde bez výhry. Aby nevyhrál, potřebuje prohrát v každém z deseti kol. Šance prohry je v každém kole jedna mínus šance výhry, a tedy se postupně o \(1.5 \%\) za kolo snižuje.
Pravděpodobnost, že odejde s výhrou, je \(1 - 0,985 \cdot 0,97 \cdot\) … \(\cdot 0,865 \cdot 0,85 = \frac{4 655 331 787 877 964 201}{8 000 000 000 000 000 000} \approx 0,58192\).
20. Milostné trojúhelníky:
Máme-li dva trojúhelníčky \(abcdef\) a \(ghijkl\), na obrázku vlevo, definujeme na nich násobení po prvcích tak, jak je vidět na obrázku vpravo. Mějme trojúhelník \(T\), který má za prvky čísla 0, 0, 0, 1, 2, 3. Jaký největší součet prvků může mít trojúhelník \(T^3=(T\cdot T)\cdot T\)?

Řešení
Označme prvky trojúhelníku \(T\) postupně \(a\), \(b\), \(c\), \(d\), \(e\), \(f\) tak, jako v trojúhelníku na obrázku. Výpočtem pak snadno zjistíme, že prvky \(T\cdot T\) jsou \(af\), \(c^2\), \(be\), \(af\), \(be\), \(d^2\), prvky \(T^3\) zase \(af^2\), \(bce\), \(c^2e\), \(ad^2\), \(b^2e\), \(adf\) (v tomtéž pořadí, shora dolů, zleva doprava). Součet prvků \(T^3\) je tudíž \(S=a\cdot(d^2+df+f^2)+e\cdot(b^2+bc+c^2)\). Zjevně nemá smysl trojici nenulových čísel dělit mezi tyto sčítance, chceme-li výstup maximalizovat; bez újmy na obecnosti tedy \(b=c=e=0\). Z výsledných možností \(S_1 = 1\cdot(4+6+9)=19\), \(S_2 = 2\cdot(1+3+9)=26\) a \(S_3 = 3\cdot(1+2+4)=21\) je největší \(26\).
21. Náhrdelník:
Anička si chce udělat náhrdelník z korálků. Má \(2\) červené, \(2\) modré, \(4\) zelené a \(4\) žluté. Kolik různých náhrdelníků si může vytvořit, pokud by ráda použila všechny korálky? Dva náhrdelníky jsou různé, jestliže nelze po jejich nasazení na krk vytvořit dva identické pouze posouváním korálků po šňůře.
Řešení
Náhrdelník si můžeme představit jako pravidelný dvanáctiúhelník se zafixovaným středem. Stejně jako v zadání pak jsou dva náhrdelníky považovány za stejné, pokud existuje nějaká rotace dvanáctiúhelníku podle středu tak, že nám zobrazí jedno rozmístění na druhé.
Nejprve uvažujme kolik existuje řad korálků, za předpokladu, že žádné dva korálky nejsou stejné. To je jednoduchá permutace a existuje tedy \(12!\) takových uspořádání.
Když bychom se nyní pokusili tyto korálky uspořádat do dvanáctiúhelníku, můžeme si všimnout, že při roztrhnutí
nějaké strany dvanáctiúhelníku (a návratu k obyčejné řadě korálků) dostaneme pro libovolné dvě různé strany různé permutace. Poskládáním do dvanáctiúhelníku se nám tak počet permutací dvanáctkrát zmenší a máme \(\frac{12!}{12} = 11!\) možností. Vzhledem k unikátnosti korálku bude počet náhrdelníků roven počtu dvanáctiúhelníků.
Když nyní korálky obarvíme dle zadání, využijeme pravidla pro permutaci s opakováním a určíme, že existuje \(\frac{12!}{{4!}^2\cdot {2!}^2}\) řad korálků. Obdobnou úvahou bychom došli k \(\frac{11!}{{4!}^2\cdot {2!}^2}\) dvanáctiúhelníkům, ovšem zde již musíme uvažovat případy, kdy z více dvanáctiúhelníků vznikne jeden náhrdelník.
Jelikož máme pouze \(2\) červené korálky, musí být ve dvanáctiúhelníku tato dvojice naproti sobě, jestliže chceme, aby se na sebe zobrazily rotací (konkrétně o \(180^{\circ}\)). Obdobně máme jednoznačně určené i ostatní barvy.
Můžeme tedy pozorovat, že jestliže je dvanáctiúhelník s doplněnými korálky symetrický podle nějaké osy, potom existuje nějaký (právě jeden) jiný dvanáctiúhelník, jejž je možno na původní zobrazit rotací. Tvrzení je dokonce ekvivalence.
Jestliže tedy daný dvanáctiúhelník není symetrický podle žádné osy, vztahuje se na něj stejný postup jako dříve. Pokud je symetrický podle nějaké osy, dává vzniknout stejnému náhrdelníku jako právě jeden jiný symetrický dvanáctiúhelník a navíc tento dvanáctiúhelník vznikl pouze z \(\frac{12}{2} = 6\) řad (řady jsou po dvou totožné).
Pokusme se nyní určit počet dvanáctiúhelníků s alespoň jednou symetrií podle osy. Zvolme osu procházející středem některé dvojice stran dvanáctiúhelníku (řešení by bylo identické pro osu procházející vrcholy). Po doplnění korálků do vrcholů v jedné polorovině je již jednoznačné doplnění druhé poloroviny. Celkem tedy stačí doplnit \(6\) korálků - \(1\) červený, \(1\) modrý, \(2\) žluté a \(2\) zelené. Zde se opět jedná o permutaci s opakováním a řad, ze kterých vzniknou symetrické dvanáctiúhelníky je \(\frac{6!}{{2!}^2} = 180\). Počet symetrických dvanáctiúhelníků tak bude \(\frac{180}{6} = 30\). Řešení nám tedy ukazuje, že s původním postupem bychom symetrických dvanáctiúhelníků našli o \(15\) méně, a tedy jich tento počet musíme následně přičíst.
Celkově máme \(\frac{11!}{{4!}^2\cdot {2!}^2} + 15 = 17340\) různých náhrdelníků.
22. Liché funkce:
Ráďa vymýšlí letošní Brkosí plakát, na který by chtěla napsat nějakou hezkou lichou funkci z celých do celých čísel. Zatím se rozhodla, že chce, aby pro ni platilo: \[\begin{aligned} f(n) &= f(n+2024) \\ f(n) &= - f(-n) \\ f(n) &\leq |n| (\text{ mod } 23)\end{aligned}\] Z kolika funkcí si může vybrat? Jako výsledek zadejte počet prvočísel v rozkladu počtu funkcí na prvočísla. Stejná prvočísla se počítají tolikrát, kolikrát se vyskytují.
Řešení
Máme tři podmínky: funkce je periodická s periodou 2024, lichá a shora omezená. Pozorujeme, že \(2024 = 23 \cdot 88\). Dále pozorujeme, že i když je funkce omezená explicitně jen shora, omezení zdola plyne z lichosti. Kdyby např. \(f(2) = -3\), muselo by se \(f(-2) = 3\), což porušuje podmínku. Také pozorujeme, že periodicita je aplikována v jednom směru, ale lichost a omezení ve dvou – od počátku pryč. Tím pádem např. \(f(2023) = f(-1)\), \(f(2023)\leq|2023|(\text{mod}23) \equiv 22 \,(\text{mod}\,23)\),ale \(f(-1)\leq|-1|(\text{mod}23) \equiv 1 \,(\text{mod}\,23)\), tudíž musíme uvažovat silnější omezení. Na funkci neklademe žádné další nároky, takže v libovolném čísle může nabývat všech hodnot, které vyhovují omezením výše. Protože je funkce periodická a lichá, zajímá nás pouze 1012 hodnot (zbytek je jimi určen), např. 0 až 1011. Rozdělíme si interval na segmenty po 23 prvcích, tolik různých je čísel modulo 23, které nás omezují. Takových segmentů je 44. Každý segment je z důvodů určených výše omezen vždy dvěma nerovnicemi, ze kterých bereme tu menší, silnější. Hodnoty jsou nezávislé, tudíž násobíme počty možností: \(1\cdot3\cdot\ldots\cdot21\cdot23\cdot23\cdot21\ldots3\), neboť v nule máme jednu možnost, v jedničce tři (-1, 0, 1), až v jedenáctce 23, ve dvanáctce vyměníme omezení a končíme ve 23. Všimneme si, že jednička nepřispěje do součinu a že zbytek se opakuje, takže můžeme psát \((3\cdot5\cdot\ldots\cdot23)^2\) Výsledek je ještě umocněn počtem segmentů, neboť jsou nezávislé, tedy \((3\cdot5\cdot\ldots\cdot23)^{88}\). Teď ještě sečteme počty prvočísel: \(3, 5, 7, 3\cdot3, 11, 13, 3\cdot5, 17, 19, 3\cdot7, 23\), celkem \(14\cdot88 = 1232\). Poznámka: Kdyby vás zajímalo, jak spočítat lichých čísel, zkuste ověřit, že platí \(3\cdot5\cdot\ldots\cdot23 = \frac{23!}{2^{11}\cdot11!}\).
23. Nesoudělní kamarádi:
Kolik existuje (neuspořádaných) dvojic nesoudělných přirozených dělitelů čísla \(24!\,\)?
Řešení
Nechť \(a, b\) je dvojice nesoudělných přirozených dělitelů čísla \(24!\). Potom pro každé prvočíslo v rozkladu platí, že je buď v nějaké přirozené mocnině obsaženo v \(a\), nebo v \(b\), nebo ani v jednom z nich. Pokud tedy prvočíslo \(p\) dělí \(24!\) v \(n-\)té mocnině, máme \(n\) možností, kam ho umístit, pokud dělí \(a\), \(n\) možností, pokud dělí \(b\), a jednu možnost, pokud nedělí ani jedno z nich. Tyto případy se vzájemně vylučují, tedy je celkem \(2n+1\) možností, pro každé prvočíslo \(p\).
Rozklad čísla \(24!\) je \(2^{22} \cdot 3^{10} \cdot 5^4 \cdot 7^3 \cdot 11^2 \cdot 13 \cdot 17 \cdot 19 \cdot 23\). Postupem popsaným výše tedy najdeme \(45 \cdot 21 \cdot 9 \cdot 7 \cdot 5 \cdot 3 \cdot 3 \cdot 3 \cdot 3 = 24 111 675\) uspořádaných dvojic dělitelů.
Tímto najdeme počet uspořádaných dvojic. Jediná dvojice obsahující dvě stejná čísla je dvojice \((1, 1)\), zbylé dvojice se vždy opakují v opačném pořadí. Neuspořádaných dvojic je tedy \(\frac{24 111 675 - 1}{2} + 1 = 12 055 838\).
24. Pevný bod přijde vhod:
O polynomu \(P\) víme, že je čtvrtého stupně a jeho vedoucí koeficient je \(-1\). Dále jsme zkoušením ověřili, že \(P(1)=1\), \(P(2)=2\) a \(P(i)=i\) (kde \(i = \sqrt{-1}\)). Určete součet absolutních hodnot jeho koeficientů, víte-li, že jde o reálná čísla.
Řešení
Uvažujme polynom \(Q(x) = P(x) - x\). Jistě \(Q(1) = Q(2) = Q(i) = 0\); známe tedy tři kořeny \(Q\). Označme čtvrtý kořen \(x_4\). Platí \(Q(x) = -(x-1)(x-2)(x-i)(x-x_4)\) a \(P(x)=Q(x)+x\); roznásobením a přičtením snadno dostaneme \(P(x)= -x^4 + (3+i+x_4)x^3 - (2+3x_4+(x_4+3)i)x^2 + (1+2x_4+(3x_4+2)i)x - 2x_4i\). Jediný přijatelný kandidát na \(x_4\) je \(-i\), jinak by kubický koeficient \(3+i+x_4\) nebyl reálný. Jeho dosazením získáme rovnost \(P(x) = -x^4 +3x^3 -3x^2 + 4x -2\); součet absolutních hodnot koeficientů je tedy \(13\).
25. Střihoruký Devy:
Jednoho dne si Devy vzal čtverec o délce strany \(1\), nůžky a až do smrti stříhal. V prvním kroku roztřetil všechny strany a odstřihnul ze čtverce čtyři rohové čtverečky s hranou délky \(\frac{1}{3}\). V každém dalším kroku roztřetil všechny strany nového útvaru a odstřihnul u každého vrcholu, jehož vnitřní úhel je \(90°\), čtvereček s hranou délky \(\frac{1}{3}\) aktuální délky kratší strany u tohoto vrcholu. Pokud by Devy stříhal nekonečně dlouho, jaký bude obsah výsledného obrazce?
Řešení
Před stříháním má čtverec obsah \(1\). Vypočítáme si, kolik Devy odstřihl, a poté to odečteme od jedničky. Prvně se zaměříme na obsah (délku strany) odstřihovaných čtverečků v každém kroku a potom na jejich počet.\
.png)
V prvním kroku zřejmě odstřihuje čtverečky se stranou délky \(\frac{1}{3}\), obsah jednoho čtverečku bude tedy \((\frac{1}{3})^2=\frac{1}{9}\). V každém dalším kroku bude mít čtvereček stranu délky \(\frac{1}{3}\) délky strany čtverečku z předchozího kroku. Obsah čtverečku bude tedy roven \(\frac{1}{9}\) obsahu čtverečku z předchozího kroku. V druhém kroku stříhá čtverečky s obsahem \((\frac{1}{9})^2\), ve třetím s obsahem \((\frac{1}{9})^3\) a tak dále.\ Nyní se podíváme na počty čtverečků. V prvním kroku jsou to 4 čtverečky. Každé odstřihnutí čtverečku nám vynutí odstřihnutí dvou čtverečků v dalším kole. Odstřihnutím čtverečku se nám na místo jednoho vrcholu v útvaru objeví 3 nové vrcholy, ze kterých bude právě u dvou pravý úhel. Počet čtverečků bude tedy v každém kroku dvojnásobný oproti tomu minulému. Ve druhém kroku to bude tedy 8 čtverečků, ve třetím 16 atd.\ Teď už nám jen zbývá to všechno spojit. Devy stříhá do nekonečna, napovídá nám to tedy na nekonečnou řadu. V prvním kroku ustřihne \(4\cdot \frac{1}{9}\) papíru, ve druhém \(8\cdot (\frac{1}{9})^2\), ve třetím \(16\cdot(\frac{1}{9})^3\) papíru a tak dále. Bude to tedy geometrická řada s koeficientem \(q=\frac{2}{9}\) a protože koeficient je (v absolutní hodnotě) menší než 1, můžeme použít vzoreček \(\sum_{n=0}^\infty a_1\cdot q^n=a_1\frac{1}{1-q}\), kde \(q\) je náš již známý koeficient a \(a_1\) je první člen posloupnosti, tj. \(a_1=\frac{4}{9}\). Dostáváme tedy: \[\sum_{n=0}^\infty \frac{4}{9}\cdot (\frac{2}{9})^n=\frac{4}{9}\frac{1}{1-\frac{2}{9}}=\frac{4}{9}\frac{1}{\frac{7}{9}}=\frac{4}{9}\frac{9}{7}=\frac{4}{7}\] Vypočítali jsme obsah papíru, který Devy odstřihne. Obsah výsledného útvaru bude tedy \(1-\frac{4}{7}=\frac{3}{7}.\)
26. Okopávat trojúhelníkovou zahradu zní jako dřina:
Bratři zdědili zahradu ve tvaru tětivového deltoidu a rozhodli se si ji rozdělit na čtyři trojúhelníky pomocí úhlopříček. Víme, že největší vzdálenost, kterou má vrchol zahrady od průsečíku úhlopříček, je jedna. Dále víme, že poměr obsahu kružnice opsané této zahrady ku obsahu zahrady je \(2:1\). Jaký je obsah nejmenšího trojúhelníku ze všech čtyř (uspořádáno pomocí \(\le\))?
Řešení
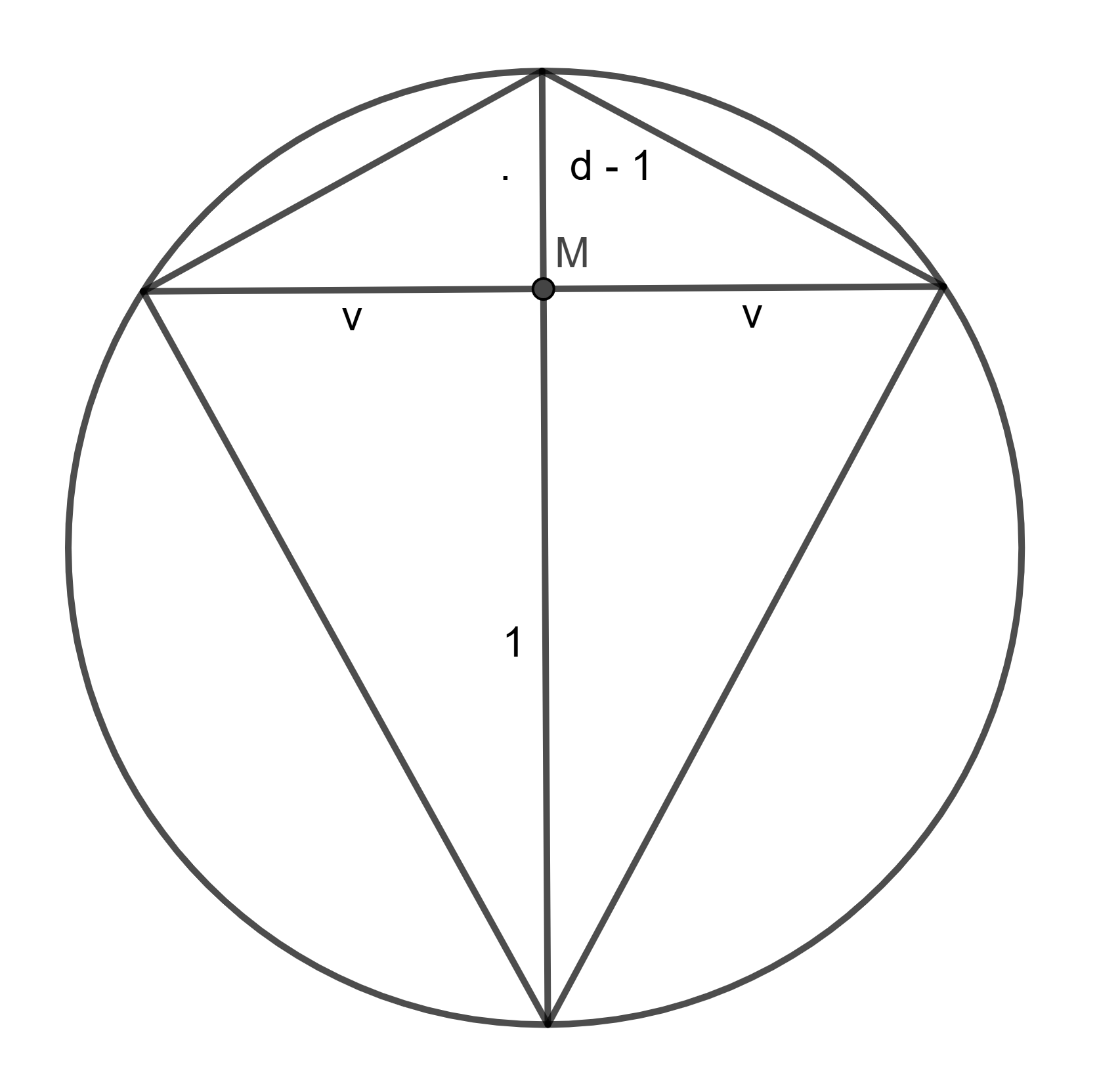
Označme si délku delší úhlopříčky \(d\) a polovinu kratší úhlopříčky \(v\). Největší vzdálenost od průsečíku k vrcholu musí být na delší z úhlopříček, protože ta je průměrem kružnice opsané a kratší úhlopříčku půlí. Ze zadání víme, že obsah deltoidu je polovinou obsahu kružnice, tedy platí:
\[2\cdot d\cdot v = \frac{\pi \cdot d^2}{4}\] \[v = \frac{\pi \cdot d}{8}.\]
Z eukleidovy věty o výšce dostaneme vztah \[v^2=(d-1)\cdot 1\] \[v^2 + 1=d.\]
Dohromady \[v=\frac{\pi \cdot (v^2+1)}{8}\] \[\pi v^2 - 8v + \pi = 0\] \[v =\frac{8 \pm \sqrt{64 - 4\pi^2}}{2\pi}\] \[v =\frac{4 \pm \sqrt{16 - \pi^2}}{\pi}.\]
Obsah malého trojúhelníku vyjádříme jako \[S=\frac{(d-1)\cdot v}{2}=\frac{v^3}{2}\] \[S=\frac{(\frac{4 \pm \sqrt{16 - \pi^2}}{\pi})^3}{2}.\]
Řešení této rovnice vycházejí asi \(4.379591\) a \(0.057082\). Zbývá se podívat, zda platí podmínka, kterou jsme v řešení ještě nevyužili – že úsečka délky \(1\) je nejdelší, tedy \(d-1\le 1\). V prvním případě dostáváme \(d = 5.24922\), v druhém \(d=1.23534\), a tedy jen druhá možnost je řešením úlohy.
27. Skákačka:
Lea hraje skákací hru, kde panáček běží stále doprava a pomocí žebříků se vertikálně přesouvá mezi patry a sbírá mince. Jeden level je dlouhý \(2024\) kroků. Žebříky jsou v pravidelných intervalech po \(44\) krocích, poslední vede do cíle a na startu není. Na každém žebříku musí změnit patro právě o \(1\). Panáček začíná v nejnižším patře, kde se nachází i cíl. Pater má hra celkem \(24\). Kolika způsoby mohla Lea hru proběhnout, když víme, že panáček proběhl v nejnižším patře právě dva úseky včetně startovního?
Řešení
Nejprve si vypočítáme, že celkem je ve hře 46 žebříků, proto nás nemusí nijak trápit podmínka, že hra má 24 pater (nestihli bychom dojít nahorů a zase zpět dolů). Jediná podmínka je tedy, že nesmíme jít dolů, pokud jsme ve spodním patře, a že musíme právě dvakrát jít po spodním patře, přičemž poprvé se to vždy stane už před prvním žebříkem. Nejlépe se úloha řeší se znalostí Catalanových čísel. Představme si prvně, že v zadání není omezení na spodní patro. Potom by správná odpověď byla 23. Catalanovo číslo. (Toto číslo udává například počet možností, jak se ve čtvercové síti \(23\times 23\) dostat z levého dolního rohu do pravého horního, aniž bychom překročili diagonálu.) Evidentně tento popis odpovídá naší úloze, kde chodíme nahoru a dolů, aniž bychom měli vícekrát cestu dolů než nahoru. Řešení této úlohy by tedy bylo \(C_{23}\), tedy 23. Catalanovo číslo. My však potřebujeme úlohu modifikovat tak, abychom právě jednou šli po spodním patře. Řekněme, že \(n\)-tým žebříkem dojdeme na spodní patro a \(n+1\). žebříkem opět vylezeme nahoru na první. Potom nutně před \(n\)-tým žebříkem jsme v prvním patře, stejně jako před druhým žebříkem – tento úsek musíme ujít, aniž bychom slezli na první patro. To si můžeme představit tak, že první patro je teď naše spodní a nesmíme se dostat pod něj. Tento počet je tedy \(C_{\frac{n}{2}-1}\). Stejně tak počet cest od \(n+1\). žebříku, které nikdy nevedou přes první patro, je \(C_{22-\frac{n}{2}}\). Nyní pouze zbývá sečíst součiny těchto dvou Catalanových čísel. To zvládneme s Wolframem, nebo si zjistíme vzorec na počítání s Catalanovými čísly \(C_{k+1}=\sum_{i=0}^{k}C_i\cdot C_{k-i}\) a dostaneme výsledek \(C_{22}\). Stačí si najít dvacáté druhé Catalanovo číslo, což je 91482563640.
28. Tetromino:
Vyplňte tabulku \(6\times 6\) devíti tetrominy z obrázku tak, aby v každém poli bylo právě jedno číslo. Navíc platí, že čísla na krajích tabulky udávají součin nebo součet čísel v příslušném řádku či sloupci. Právě \(6\) čísel určuje součin a právě \(6\) součet. Tetromina lze otáčet, nelze je ovšem zrcadlově převracet. Pozice prvního tetromina je dána obrázkem. Jako řešení zadejte čísla v druhém a pátém řádku tabulky (postupně po řádcích zleva doprava), přičemž mezi každé dvě čísla vepište jedničku, pokud se mezi nimi nachází stěna tetromina a nulu, pokud ne. Řádky ničím neoddělujte.
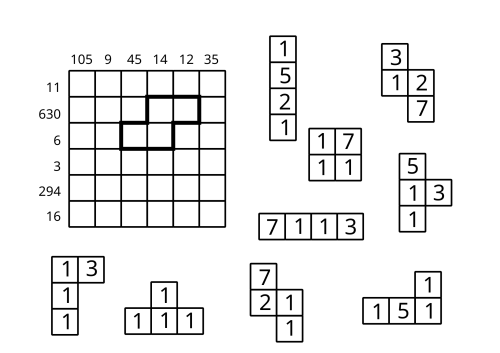
Řešení
Nejdříve si uvědomíme, že součet šesti čísel z daných tetromin musí být nejméně \(6=>\) ve \(4.\) řádku číslo \(3\) znázorňuje součin. Dále, součtem šesti největších čísel v tetrominech (\(4\times 7 + 2\times 5=38\)) dostáváme maximální součet těchto čísel (který reálně do jednoho řádku/sloupce ani nejde poskládat) \(=>\) všechna čísla větší než \(38\) jsou součiny (\(105,45,630,294\)). Pokud se zaměříme na poslední sloupec, zjistíme, že kvůli rozdělení čísel do tetromin nejsme schopni v krajním sloupci dostat součet větší než \(30\) => \(35\) je součin.
Součiny: \(105,45,35,630,3,294\)
Součty: \(9,14,12,11,6,16\)
Pomocí tohoto můžeme vyplnit \(3.\) řádek jedničkami, což nám jasně určuje, že \(1.\) tetromino, které je znázorněno v zadání, je \(H\). To nám jednoznačně určuje celý \(5.\) sloupec, který je doplněný jedničkami (\(7+5\times 1=12\)). Následně určíme, která čísla musejí být ve kterých řádcích resp. sloupcích. Součiny jednoduše rozložíme na prvočísla (tetromina obsahují pouze prvočísla) a doplníme jedničkami do šesti čísel. Pokud se zaměříme na řádky, máme určené tři sedmičky, zbývá jedna a máme na výběr \(1.\) a poslední řádek. V \(1.\) však být nemůže, protože \(11-7=4\), ale chybí nám ještě doplnit \(5\) čísel \(=>\) \(7\) bude v posledním řádku. Zároveň nám chybí umístění dvou pětek, přičemž v posledním řádku nám zbývá součet \(9\) a v prvním je stále \(11=>\) v obou řádcích bude právě jedna pětka. Následným dopočtem (\(1.\) řádek \(5,2,1,1,1,1\); poslední \(7,5,1,1,1,1\)) jsme určili čísla všech řádků. Ve sloupcích nám chybí určit jednu sedmičku. Máme na výběr pouze \(2.\) a \(4.\) sloupec, ve druhém je však součet \(9\), takže \(7\) musí být v \(5.\) sloupci spolu se dvěma dvojkami (jedna už tam je) a třemi jedničkami. K dispozici máme už jen jednu \(2\), takže \(2.\) sloupec bude tvořen čísly \(3,2,1,1,1,1\).
Nejdříve se zaměříme na tetromino \(A\). Pokud bychom ho chtěli dát někam doprostřed tabulky (jeho delší strana nesplývá se stranou tabulky), musela by se pětka nacházet v \(2.\) řádku, \(3.\) sloupci, což není možné kvůli již určenému tetrominu \(H\). \(A\) bude tedy na kraji
, přičemž v posledním řádku ani sloupci nemůže být, kvůli \(2\), která je v \(A\), ale v těchto sloupcích být nemůže \(=>A\) leží v prvním řádku tak, že \(5\) se nachází ve \(3.\) sloupci, \(2\) bude ve \(2.\) nebo \(4.\) sloupci a jinde (\(1.,5.,6.\) sloupec) musí být jedničky.
Dále můžeme vyloučit, že by \(5\) byla ve \(2.\) řádku, \(1.\) sloupci. Ani tetromino \(E\) ani \(I\) na dané místo nesedí (kryjí se s jinými nebo nesedí čísla s již vyplněnými nebo vznikne nevyplněný prostor (např. \(2\times 1\)), který nejsme schopni vyplnit) \(=>\) na druhém řádku musí být pětka v posledním sloupci. Tetromino \(E\) tam být nemůže kvůli jedničkám v 5. sloupci \(=>\) použijeme tetromino \(I\), které však nevíme, jak bude natočené také kvůli \(5.\) sloupci. Tetromino \(E\) tedy musí ležet v levém dolním rohu tak, že v posledním řádku bude mít \(3\) pole (pokud by bylo postavené
, v \(1.\) sloupci by byly \(4\) jedničky, což už být nemůže).
Tetromino \(D\) musí být v prvním sloupci \(2.-5.\) řádku sedmičkou dole (jinak se nevleze nebo neodpovídá číslům, které musí v daných sloupcích a řádcích být). Proto můžeme určit, že \(A\) bude v \(1.-4.\) sloupci (jinak by \(1.\) pole zůstalo prázdné) a \(I\) bude otočené tak, že bude zabírat poslední \(2\) volná pole v řádku. Ve \(2.\) řádku nám zbývá doplnit \(3,1\) – tato čísla obsahují už jen tetromina \(B,F\) – z těchto dvou vyhovuje pouze \(F\). Poslední trojka musí být ve \(4.\) řádku \(3.\) sloupci, přičemž \(B\) pak musí pokračovat směrem dolů, aby se sedmička nekryla s již určenou jedničkou. Poslední \(7\) musí být v \(5.\) řádku \(6.\) sloupci. Abychom byli schopni vložit do tabulky i tetromino \(G\), \(C\) musí být v rohu.

29. Polská množina:
Štěpán má třicetiprvkovou množinu Bober, jejíž prvky jsou přirozená čísla. Řekneme, že množina gryze, pokud pro právě půlku jejích podmnožin platí, že součin jejích prvků je dělitelný dvěma, pro právě tři čtvrtiny podmnožin platí, že součin jejích prvků je dělitelný třemi, a právě pro sedm osmin podmnožin platí, že součin jejích prvků je dělitelný pěti. Jaký nejmenší součet prvků může mít množina Bober, která gryze?
Řešení
Součin čísel je dělitelný nějakým prvočíslem \(p\) právě tehdy, když je dělitelné \(p\) alespoň jedno z nich. Pokud bude právě jedno z třiceti čísel dělitelné \(p\), bude určovat, zda bude součin podmnožiny a dělitelný \(p\), nebo nebo ne. Kromě něj musíme pro každý ze zbývajících \(29\) prvků určit, zda v dané podmnožině a bude, nebo ne: \(2^{29}\) možností. \(2^{29}\) podmnožin bude mít součin dělitelný \(p\), a \(2^{29}\) ne. Vychází to tedy, že právě polovina bude dělitelná \(p\).
Podobně, pokud bude \(k\) čísel dělitelných \(p\), kde \(k\) je nějaké přirozené číslo, budou určovat, zda součin podmnožiny bude dělitelný \(p\). Pokud nebude žádné číslo dělitelné \(p\) v dané podmnožině, tak ani součin jím nebude dělitelný. Pokud alespoň jedno z nich bude v dané podmnožině, jejich součin dělitelný \(p\) bude; to je \(2^k - 1\) možností z \(2^k\). Pro \(k = 2\) jsou to tři ze čtyř, pro \(k = 3\) je to sedm z~osmi, atd.
Aby gryžal, budeme tedy potřebovat, aby v něm bylo právě jedno sudé číslo, dvě čísla dělitelná třemi, a tři čísla dělitelná pěti. Tato čísla se mohou překrývat (např. 5, 15, 30 splňují všechny tři požadavky). Budeme tedy ještě potřebovat \(24\) až \(27\) čísel navíc, která nejsou dělitelná dvěma, třemi ani pěti. Záleží nám pouze, aby byla co nejmenší, takže tady je 27 nejmenších z nich:
\[\begin{matrix} 1& 7& 11& 13& 17& 19& 23& 29& 31& 37 \\ 41& 43& 47& 49& 53& 59& 61& 67& 71& 73 \\ 77& 79& 83& 89& 91& 97& 101\\ \end{matrix}\] Jelikož tato čísla začínají být docela velká, intuitivně jich chceme mít v ovi co nejméně. Odpíchneme se tedy od součtu takového, když se čísla splňující gryžací podmínky nebudou krýt. Mějme tedy tři čísla dělitelná pěti, pak dvě čísla dělitelná třemi a jedno sudé, všechna různá. Nejmenší číslo dělitelné dvěma, ale ne třemi ani pěti, je jednoduše \(2\). Nejmenší dvě čísla dělitelná jen třemi jsou \(3\) a \(9\). Nejmenší čísla dělitelná pěti, ale ne dvěma či třemi, jsou \(5\), \(25\), \(35\). Součet těchto šesti čísel a dvaceti čtyř nejmenších ze seznamu je \(1159\). Ukážeme, že tento součet je nejmenší možný. Pokud bychom čísel potřebných kvůli gryžacím podmínkám využili pět nebo míň, museli bychom použít alespoň dvacet pět nejmenších čísel ze seznamu, a ta samotná mají součet \(1171\), tedy víc, než jsme už postavili.
Výsledkem tedy je \(\mathbf{1159}\), a to s následujícím výběrem čísel: \[\begin{matrix} 2 \\ 3& 9 \\ 5& 25& 35 \\ 1& 7& 11& 13& 17& 19& 23& 29& 31& 37 \\ 41& 43& 47& 49& 53& 59& 61& 67& 71& 73 \\ 77& 79& 83& 89& \\ \end{matrix}\]
30. Zkouška z Finančky:
Tonda píše zkoušku z finanční matematiky. Zkouška má \(4\) úlohy, každá má jen \(1\) správnou odpověď. První je za \(10\) bodů a má \(3\) možné odpovědi, druhá je za \(25\) bodů a má \(4\) možné odpovědi, třetí je za \(30\) bodů a má \(5\) možných odpovědí a čtvrtá je za \(35\) bodů a má \(6\) možných odpovědí. Tonda se na zkoušku nestihl naučit, a tak odpovídá náhodně, uniformě (každou odpověď vybere se stejnou pravděpodobností). Jaká je pravděpodobnost, že dostane alespoň \(50\) bodů a projde?
Řešení
Uvažme postupně všechny způsoby, jak může Tonda dostat alespoň 50 bodů. Odpoví-li na čtvrtou otázku správně, pak musí odpovědět správně i na alespoň jednu z druhé a třetí otázky. První otázka v tomto případě nehraje roli. Pokud na čtvrtou otázku neodpoví správně, ale na třetí ano, pak musí také zodpovědět správně otázku druhou. První opět nehraje roli. Pokud neodpoví správně ani na čtvrtou, ani na třetí otázku, může získat nanejvýš 35 bodů, a tedy jistě neprojde. Tyto dvě situace se vzájemně vylučují a jejich pravděpodobnosti jsou \(\frac{1}{6} \left(1- \frac{4}{5}\cdot\frac{3}{4}\right) = \frac{1}{15}\) a \(\frac{5}{6} \frac{1}{5} \frac{1}{4} = \frac{1}{24}\); celková pravděpodobnost složení zkoušky je tedy jejich součet, \(\frac{13}{120}\).