| Časový rozestup 40 s |
Zadání XVII. ročníku
1. sada
Sada 1
Konec odevzdávání: 24. listopadu 2025 17:00
1. Famfrpál:
Brkos tým hraje famfrpál ve složení Tonda, Ráďa, Lea, Áďa, Kuba.
Tonda vždy hraje 1 minutu, potom fauluje.
Ráďa vždy hraje 3 minuty, potom fauluje.
Lea vždy hraje 6 minut, potom fauluje.
Áďa vždy hraje 9 minut, potom fauluje.
Kuba je dobrák a nefauluje.
Hrací doba je 200 minut a trest za faul jsou 3 minuty na trestné lavici. Určete kolik minut budou na hřišti právě 2 hráči z Brkos týmu.
Řešení
Tondova přítomnost na hřišti se bude cyklit po čtyřech minutách, Rádina po šesti, Leina po devíti a Ádina po dvanácti. Kubu řešit nemusíme, ten bude na hřišti celou dobu. (Stačí nám tedy vyřešit, kolik minut bude na hřišti právě jeden ze zbylých čtyř hráčů.) Nejmenší společný násobek těchto čísel je 36. To bude tedy délka cyklu všech hráčů dohromady. (V 37. minutě budou na hřišti stejní hráči jako v první atd.)
Uděláme si tedy tabulku přítomnosti hráčů na hřišti prvních 36 minut:

Vidíme, že se za \(36\) minut na hřišti objeví právě jeden hráč osmkrát a protože \(200 = 5\times36 + 20\), dostáváme, že celkový počet minut, kde budou na hřišti právě dva hráči je: \[5\times8 + 5 = 45\]
2. Pekáč buchet:
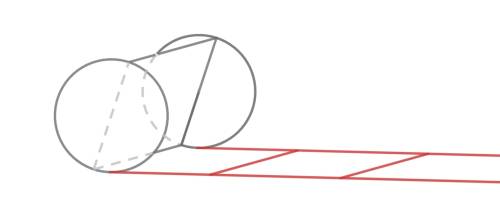
Ráďa upekla buchtu o rozměrech \(49\times31,5\) cm a chce ji nakrájet na co největší stejně velké čtverečky. Má k tomu speciální pomůcku, která jí krájení značně ulehčí. Skládá se ze dvou koleček (jak na krájení pizzy), která jsou spojená jedním obdélníkem, který zajistí, že nevykrojí pruhy buchty, ale rovnou čtverečky (viz obrázek). Jak velký musí být poloměr koleček (v cm)?
Řešení
Jako první musíme zjistit, jak velké čtverečky Ráďa bude vykrajovat. Zřejmě by mohla dělat čtverečky o straně délky \(0,5\) cm, nepůjde to ale i na větší čtverečky? Ano, půjde. Když si představíme, že má dvakrát větší plech, tzn. \(98\times63\) cm, můžeme si všimnout, že NSD \(98\) a \(63\) je \(7\). Tento plech by šel tedy rozkrájet na stejně velké čtverečky se stranou délky maximálně sedm. Náš dvojnásobně malý plech tedy lze rozkrájet na stejně velké čtverečky se stranou délky maximálně \(3,5\) cm. Označme si \(o\) jako obvod našeho kolečka, z obrázku ze zadání vidíme, že musí platit: \[o=2\times3,5\] \[2\pi r=7\] \[r=\frac{7}{2\pi}=1,1140846\dots\]
3. Peťa zasadila fazoli:
Peťa zasadila fazoli. Fazole byla ale kouzelná a přes noc vyrostla výš než čekala a z listů při tom vytvořila schodiště do nebe. Když se na ni člověk podívá z vrchu, tak špičky všech listů jdou vidět (míří každý jiným směrem) a tvoří pravidelný 70-ti úhelník. Po listech se dá lézt, v každé výšce je pouze jeden a mezi výškově následujícími listy je vždy stejný úhel otočení. Fazole je ale záludná, snaží se, aby tento úhel \(\alpha\in(0,\pi)\) byl co největší a lezec musel co nejvíckrát obkroužit stonek a zatočila se mu hlava. Kolikrát se Peťa projde nad prvním listem, než vyleze do nebe (počítáme-li i první list a Peťa potom zůstane stát na posledním listu)?
Řešení
Při pohledu shora vidíme pravidelný \(70\)úhelník, jehož vrcholy dělí plný úhel na \(70\) částí. Víme, že Peťa v každém kroku z listu na list překoná stejný počet \(x\) těchto částí, a to co nejvíce (maximálně \(35\)).
Nejprve si uvědomme, že tento počet musí být nesoudělný se \(70\). Pokud by nebyl a existovalo kladné \(d>1\) dělící \(x\) i \(70\), dostala by se Peťa po \(\frac{70}{d}\) krocích opět na úroveň prvního listu. To znamená, že by fazole netvořila \(70\)úhelník, ale jen \(\frac{70}{d}\)úhelník.
Největší přirozené číslo menší nebo rovno \(35\), které je se \(70\) nesoudělné, je \(33\). Opravdu, pokud od sebe listy budou vzdálené \(33\) vrcholů, vytvoří díky nesoudělnosti \(70\) a \(33\) schodiště až k poslednímu listu (první násobek \(33\) dělitelný \(70\) bude až \(33\cdot 70\)). Dohromady se tedy Peťa kolem osy otočí o \(69\cdot 33\) vrcholů, což odpovídá \(32\) plným otočkám, při nichž projde nad prvním listem. Při započtení prvního listu dostáváme výsledek \(33\).
4. Pěting:
Jaké je nejmenší kladné celé číslo složené pouze z \(0\) a \(5\), které je dělitelné sedmi?
Řešení
Pomůcka pro dělitelnost sedmi je, že můžeme z čísla odebrat poslední číslici, vynásobit ji dvěma a odečíst od začátku čísla. Pomocí tohoto můžeme rychleji kontrolovat postupně čísla od 0, která obsahují 0 a 5.
Postupně máme čísla:
\(0,\:5,\:50\:(5), \:55 \:(-5), \:500 \:(50), \:505 \:(40), \:555 \:(45), \:5000 \:(500), \:5005 \:(490 \:\checkmark)\)
Takže řešením je \(5005\).
5. Čtverečky:
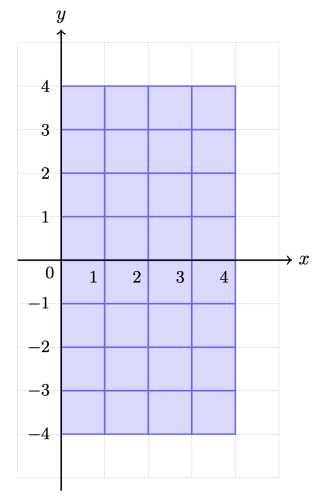
Mějme běžnou kartézskou síť bodů. Vybereme si čtverečky (ohraničené přímkami na celočíselných hodnotách), které jsou vpravo od počátku a žádný čtvereček není dále než za/nad/pod hodnotou \(x=4, y=4\) a \(y=-4\). Kolik různých přímek s celočíselnými sklony a celočíselnými posuny z intervalu \(\langle-4,4\rangle\) \((y = ax + b\), kde \(a \in \mathbb{Z}, b \in \{-4,-3,-2,-1,0,1,2,3,4\})\) můžeme vytvořit, aby procházela přímka vždy alespoň dvěma sloupci a zároveň alespoň dvěma řádky vybraných čtverečků? Čtverečkem prochází přímka, jen pokud prochází vnitřkem čtverečku.
Řešení
V zadání máme omezené posuny, tak můžeme začít například od \(-4\) a zkoušet, kolik může vzniknout přímek s celočíselným sklonem. Ze začátku si můžeme uvědomit, že sklon nikdy nemůže být \(0\) kvůli poslední větě zadání. U posunu \(-4\) zároveň víme, že musí být sklon kladný, abychom prošli nějakým barevným čtverečkem. Po zkoušení zjistíme, že nám vyhovují sklony \(1,\: 2,\: 3,\: 4,\: 5,\: 6,\: 7\). Od sklonu \(8\) a výše projdeme jen jedním sloupečkem. S posunem \(-4\) máme tedy \(7\) možností.
Dále pokračujeme s posunem \(-3\). Zde už je možnost sklonu \(-1\), ale ten projde jen jediným sloupcem, takže nevyhovuje zadání. Musíme mít tedy zase kladné sklony a vyhovují nám \(1,\: 2,\: 3,\: 4,\: 5,\: 6\). \(7\) a vyšší už zase projde jen jedním sloupcem. Máme tedy \(6\) možností.
Pro posun \(-2\) máme už možnost sklonu \(-1\), ale více záporné nevyhovují. Naopak kladné sklony mohou být \(1,\: 2,\: 3,\: 4,\: 5\). Máme tedy \(6\) možností. Pro posun \(-1\) máme možnosti \(-2,\: -1,\: 1,\: 2,\: 3,\: 4\) a tedy \(6\) možností. Dohromady máme \(7 + 6 + 6 + 6 = 25\) možností. Počet možností pro posuny \(1,\:2,\:3,\:4\) je stejný, protože je příklad symetrický. Zbývá nám už jen zjistit počet možností pro posun \(0\). Tam máme možnosti \(-3,\:-2,\:-1,\:1,\:2,\:3\), kterých je 6. Dohromady máme tedy \(25 + 25 + 6 = 56\) možností přímek.
6. Ďábelský had:
Ďábelský had je omotaný kolem kmenu stromu průměru \(1\) m. Je tam omotaný \(15\times\) tj, hlava hada míří na opačnou stranu než jeho ocas, a současně je o \(20\pi\) m výš, než jeho ocas. Jak je ďábelský had dlouhý (v m)?
Řešení
Povrch stromu, na kterém je had omotaný, můžeme uvažovat rozmotaný jako obdélník o jedné straně odpovídající výškovému rozdílu mezi hlavou a ocasem, tzn. \(20 \pi\),m, a druhé straně o délce počet otočení krát obvod stromu tzn. \(15\cdot\pi\),m. Na úhlopříčce tohoto rozmotaného obdélníku poté leží had, dlouhý dle Pythagorovy věty \(\sqrt{(20\pi)^2+(15\pi)^2} = \pi \sqrt{625} = 25\pi = 78.53982\) metrů.
7. Přežívající žáby:
Žába Bublina se narodila zároveň se třemi dalšími sourozenci. Pro každou ze čtyř žab platí, že šance že přežije následující rok, je \(1 - 0.02 \cdot\) {počet živých sourozenců bez sebe sama}. Jaká je šance, že Bublina přežije dva roky?
Řešení
Značení \(\binom{a}{b}\) zde znamená počet způsobů, jak vybrat \(b\) jedinců ze skupiny velikosti \(a\) bez ohledu na pořadí výběru. V obou využitých případech jde zjevně o číslo \(3\).
Pokud první rok zahynou všichni tři sourozenci a Bublina přežije, jistě přežije i~druhý rok. Pravděpodobnost tohoto jevu je \(0.06^3\cdot0.94\cdot 1\); každý ze sourozenců zahyne s pravděpodobností \(0.06\), Bublina přežije s pravděpodobností \(0.94\).
Pokud první rok zahynou dva ze tří sourozenců a Bublina přežije, přežije druhý rok s~pravděpodobností \(0.98\). Pravděpodobnost tohoto jevu je tedy \(\binom{3}{2}\cdot 0.06^2 \cdot 0.94^2 \cdot 0.98\); pro každou možnou dvojici může Bublina přežít zvlášť.
Pokud první rok zahyne jediný sourozenec a Bublina přežije, přežije druhý rok s~pravděpodobností \(0.96\). Pravděpodobnost tohoto jevu je \(\binom{3}{1}\cdot 0.06 \cdot 0.94^3 \cdot 0.96\).
Pokud první rok nezahyne žádný sourozenec a Bublina přežije, přežije druhý rok s~pravděpodobností \(0.94\). Pravděpodobnost tohoto jevu je \(0.94^4 \cdot 0.94\).
Tyto možnosti se vzájemně vylučují a jiným způsobem se Bublina nemůže druhého roku dožít; musí přežít první i druhý, a v prvním může zahynout nula až tři sourozenci. Celková pravděpodobnost Bublinina přežití obou let je tedy součtem pravděpodobností každé možnosti, neboli \(0.06^3\cdot 0.94 + 3 \cdot 0.06^2\cdot 0.94^2\cdot 0.98 + 3\cdot 0.06\cdot 0.94^3 \cdot 0.96 + 0.96^5 = 0.88698\).
8. Jablečná smršť:
Tonda trhá jablka ze stromu. Protože už je vysoko, musí se jednou rukou držet, proto se mu občas stane, že se s utrženým jablkem uvolní několik dalších. Konkrétně pro \(n\)-té jablko je to \(\lfloor log_3(n)\rfloor\) jablek. (\(\lfloor x\rfloor\) značí největší celé číslo, které je menší nebo rovno \(x\).) Kolik jablek spadne na zem, když nasbírá plný košík \(200\) jablek?
Řešení
Každou nasbíranou mocninu tří se počet shozených jablek zvýší. Stane se to v hodnotách \[3,9,27,81,\] další mocniny už jsou vyšší než 200. Ve výsledku máme \[2\cdot0+(9-3)\cdot1+(27-9)\cdot2+(81-27)\cdot3+(200-81+1)\cdot4=684,\] kde jsme na konci přidali 1, neboť sbíráme do dvou set včetně.
9. V síti:
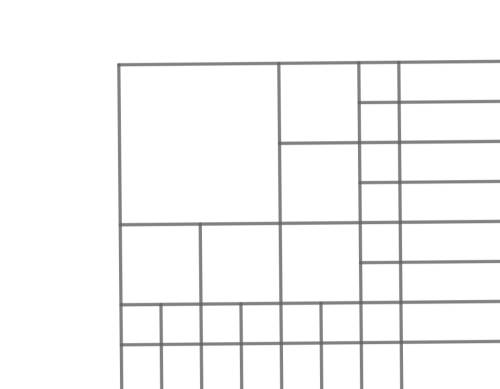
Mějme síť, která má vlevo nahoře čtverec se stranou délky \(\frac{1}{2}\), kolem něj jsou čtverce se stranou o délce \(\frac{1}{4}\), kolem nich čtverečky se stranami o délce \(\frac{1}{8}\) a tak dále, viz obrázek. Na síť házíme kolmo balónek. Pokud se balónek dotkne sítě, odrazí se a neproletí. Určete pravděpodobnost, že balónek proletí skrz síť, když víte, že jeho poloměr je \(\frac{1}{48}\) a balónek hodíme tak, že jeho střed bude vždy v síti.
Řešení
Celá síť je čtverec \(1 \times 1\), abychom zjistili pravděpodobnost, že balónek proletí, musíme určit obsah plochy, kam může balónek dopadnout, aby proletěl, a podělit ho celkovou plochou sítě (to je ale v příkladu 1, takže to není potřeba).
Jak určíme obsah potřebné plochy? Začneme od největšího čtverce \(\frac{1}{2} \times \frac{1}{2}\). Aby balónek tímto čtverečkem proletěl, musí dopadnout dovnitř čtverečku dostatečně daleko od okrajů, aby se jich nedotkl. Budeme uvažovat, kam musí dopadnout střed balónku. To je mírně menší čtverec uvnitř našeho \(\frac{1}{2} \times \frac{1}{2}\), který má délku strany \(\frac{1}{2} - \frac{2}{48}\) – museli jsme odečíst \(\frac{1}{48}\) z každé strany, což je poloměr balónku. Celkově tak získáváme plochu \((\frac{1}{2}-\frac{2}{48})^2\). Dále budeme pokračovat stejně se čtverečky \(\frac{1}{4} \times \frac{1}{4}\), kterých je ale 5 podle obrázku, takže plocha uvnitř těchto čtverečků je \(5 \cdot (\frac{1}{4}-\frac{2}{48})^2\). Dalších čtverečků je 13 podle obrázku (můžeme vzít i univerzální vzorec počet předchozích čtverečků
$ + 3$). Plocha uvnitř těchto čtverečků je \(13 \cdot (\frac{1}{8}-\frac{2}{48})^2\). Poslední čtverečky, kde zbyde prostor po odečtení \(\frac{2}{48} = \frac{1}{24}\), jsou ty o velikosti \(\frac{1}{16} \times \frac{1}{16}\). Těchto je \(2 \cdot 13 + 3 = 29\) a plocha uvnitř těchto čtverečků je \(29 \cdot (\frac{1}{16}-\frac{2}{48})^2\). Menší čtverečky už jsou tak malé, že i kdyby balónek letěl středem, tak se vždy dotkne sítě.
Celkem máme tedy \((\frac{1}{2}-\frac{2}{48})^2 + 5 \cdot (\frac{1}{4}-\frac{2}{48})^2 + 13 \cdot (\frac{1}{8}-\frac{2}{48})^2 + 29 \cdot (\frac{1}{16}-\frac{2}{48})^2 = 0.52995\). Po podělení \(1\) dostáváme pravděpodobnost jako úplně stejné číslo.
10. Kdo šetří má za tři:
Terka skládá polynomy nad \(\mathbb{Z}_3\), stupně maximálně \(2\). Tzn. koeficienty těchto polynomů mohou být pouze \(0,1,2\). Hodnota polynomu se pak vyhodnotí taky v \(\mathbb{Z}_3\), tj. to bude hodnota polynomu modulo \(3\). Kolik z těchto polynomů nebude mít nad \(\mathbb{Z}_3\) kořen (tj. kořenem nebude ani \(0\), ani \(1\) ani \(2\))?
Řešení
Nejdříve si uvědomíme, že polynomy nultého stupně nemají kořeny, až na polynom \(P(x)=0\). Hned tedy máme \(2\) polynomy (\(P(x)=1\) a \(P(x)=2\)), které nemají kořen nad \(\mathbb{Z}_3\).
Dále můžeme vyřadit všechny polynomy tvaru \(P(x)=bx^2+ax\), neboť tyto polynomy mají vždy alespoň jeden kořen nad \(\mathbb{Z}_3\) a to \(x=0\).
Všechny zbylé polynomy jsou vypsané v tabulce vedle, kde vidíme, že pouze \(6\) polynomů nemá žádný kořen nad \(\mathbb{Z}_3\). Spolu s polynomy nultého stupně je jich tedy \(6+2=8\).
| \(x^2\) | x | 1 | Kořeny nad \(\mathbb{Z}_3\) |
|---|---|---|---|
| 0 | 1 | 1 | 2 |
| 0 | 1 | 2 | 1 |
| 0 | 2 | 1 | 1 |
| 0 | 2 | 2 | 2 |
| 1 | 0 | 1 | - |
| 1 | 0 | 2 | 1, 2 |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 2 | - |
| 1 | 2 | 1 | 2 |
| 1 | 2 | 2 | - |
| 2 | 0 | 1 | 1, 2 |
| 2 | 0 | 2 | - |
| 2 | 1 | 1 | - |
| 2 | 1 | 2 | 2 |
| 2 | 2 | 1 | - |
| 2 | 2 | 2 | 1 |
11. Štěpán už nejezdí autobusem:
Štěpán jezdí v Mario Kart sandboxu a snaží se nasbírat co nejvíc penízků. Jízda se odehrává v nekonečném městě tvaru čtvercové mřížky o délce hrany \(200\) metrů a zanedbatelné šířce silnice, ve kterém se na každé křižovatce na každým jejím rohu nachází penízek. Štěpán jede rychlostí \(60\) km/h, při zatáčení dokonale zachovává rychlost a nikdy necouvá ani se neotáčí o \(180^\circ\). Při jednom průjezdu křižovatkou je však schopen vzít pouze penízek po levé straně, a to pouze když zatáčí doleva. Kolik penízků může Štěpán během půlhodinové jízdy nasbírat, když začíná uprostřed cesty mezi křižovatkami?
Řešení
Štěpán za půl hodiny stihne ujet \(60\cdot0.5=30\) kilometrů, což je \(30/0.2=150\) úseků, tedy projede i \(150\) křižovatek. Nejvíc by tedy mohl vzít 150 penízků, to by musel pokaždé zatočit vlevo. To ovšem nejde, neboť po čtyřech zatočeních by mu penízky došly. Všimneme si, že po objetí bloku dokolečka můžeme jet chvilku rovně a najednou jsme v čerstvém bloku. Víc než čtyři penízky za sebou vzít nemůžeme a méně než jednu ulici navíc si potom nezajedeme, takže strategie je optimální. Z pěti úseků vždy čtyřikrát vezmeme penízek, takže získáváme celkové skóre \(150\cdot\frac45=120\).
12. Pohodová úloha:
Zadejte počet všech přirozených řešení rovnice \[x^2 + 3^y = xy\] pro které \(x<2025\).
Řešení
Pokud si zkusíme nějaké malé případy pro \(x\) a \(y\), zjistíme, že levá strana rovnice začne být příliš velká. Po prozkoušení všech malých případů jde uhodnout, že odpověď je \(0\). Pořádněji jde výsledek odvodit následovně: \[\begin{aligned} x^2 + 3^y &= xy \\ 3^y &= xy - x^2 \\ 3^y &= x(y - x)\end{aligned}\] Pokusíme se ukázat, že \(3^y > x(y-x)\), pro všechna \(x\) a \(y\). Pokud by nastalo, že \(x \ge y\), tak by \(y - x\) bylo záporné (nebo \(0\)), a tedy i celé \(x(y-x)\) bylo také záporné ( nebo \(0\)), což znemožňuje rovnost, neboť \(3^y\) je kladné. To znamená, že nám stačí uvažovat o \(x < y\). To nám dovoluje vykonat následující odhady: \[\begin{aligned} y &\ge y - x \\ y &\ge x \\ &\Downarrow \\ y^2 &\ge x(y - x)\end{aligned}\] Zbývá nám ukázat, že \(3^y > y^2\) \[\begin{aligned} y = 1 &\quad 3 > 1 \\ y = 2 &\quad 9 > 4 \\ y = 3 &\quad 27 > 9 \\ y = 4 &\quad 81 > 16 \\ y = 5 &\quad 243 > 25 \\ & \vdots \\ y = 10 &\quad 59049 > 100 \end{aligned}\] Pořádně lze tento fakt dokázat například indukcí. Pro \(y \le 5\) jsme již tento fakt spočítali, takže máme bázový případ. Předpokládejme, že platí \(3^y > y^2\), \(y \ge 5\), a pokusme se dokázat, že \(y' = y + 1\) také splňuje stejnou nerovnici \(3^{y'} > {y'}^2\). \[3^{y'} = 3^{y+1} = 3 \cdot 3^{y} > 3y^2 > 2y^2 + 5y > y^2 + 2y + 1 = (y+1)^2 = {y'}^2\]
13. Propletené kružnice:
Mějme kružnice \(k_1,k_2\) se středy \(S_1\neq S_2\) mající poloměr \(r_1\). Tyto kružnice se protínají ve dvou různých bodech \(P_1, P_2\). Označme \(\alpha = |\angle P_1 S_1 P_2| = |\angle P_1 S_2 P_2|\). Dále kružnice \(l_1,l_2\) mají středy \(P_1,P_2\) a poloměr \(r_2\). Víte, že se trojice kružnic \(k_1,l_1,l_2\) a \(k_2,l_1,l_2\) protínají v jednom bodě a také že \(r_2=\frac{1}{2} r_1\). Určete \(\alpha\). Odpověď zadejte ve stupních.
Řešení
Začneme obrázkem, který napoví:

Zkusíme vyjádřit \(r_2\) jako nějaký výraz obsahující \(r_1\) a \(\alpha\). Lze si všimnout, že úhel \(|\angle P_1AS_1|\) je pravý. Pak z vlastností goniometrických funkcí plyne \(|AP_1|=r_1\sin\frac{\alpha}{2}\) a \(|AS_1|=r_1\cos\frac{\alpha}{2}\). Víme, že \(|P_1G|=r_2\), také můžeme vyjádřit \(|AG|=|S_1G|-|S_1A|=r_1-r_1\cos\frac{\alpha}{2}\); následně z Pythagorovy věty v \(\triangle P_1AG\) dostáváme a upravujeme chtěný výraz \[|P_1G|^2 = |AP_1|^2 + |A G|^2\] \[r_2^2=r_1^2\sin^2\frac{\alpha}{2}+r_1^2\Big(1-\cos\frac{\alpha}{2}\Big)^2\] \[\frac{r_2^2}{r_1^2}=\sin^2\frac{\alpha}{2}+1-2\cos\frac{\alpha}{2}+\cos^2\frac{\alpha}{2}\] \[\frac{(\frac{r_1}{2})^2}{r_1^2}=\sin^2\frac{\alpha}{2}+1-2\cos\frac{\alpha}{2}+\cos^2\frac{\alpha}{2}\] \[\frac{1}{4}=2-2\cos\frac{\alpha}{2}\] \[\frac{7}{8}=\cos\frac{\alpha}{2}\] \[2\arccos\frac{7}{8}=\alpha\] \[\alpha=57,910048\ldots\approx57,91005\]
14. Martin zahradníkem:
Martin sází stromky. Tyto stromky jsou čtyřletky, kde každý rok na konci větve vyroste \(0, 1\) nebo \(2\) větve (pokud tam naroste \(0\) větví, je to stále považováno za konec větve). Tyto větve mohou narůst buď doprava, nebo doleva. V případě růstu \(2\) větví pak roste vždy jedna vlevo a jedna vpravo. Pokud se na stromky díváme z jednoho pohledu (symetrické stromky se nepočítají jako jeden), kolik různých stromků takto může vyrůst?
Řešení
Jelikož máme 4 roky, větve stromků budou tvořit až 4 vrstvy. Nejprve se zaměříme na první vrstvu, která je přímo u země. Jsou pro ni 4 možnosti:
Neobsahuje nic.
Je jedna větev vedoucí doprava.
Je jedna větev vedoucí doleva.
Dvě větve na obě strany.
Pro každou větev v této vrstvě ještě musíme uvažovat možnosti toho, co je nad nimi. To, co je nad nimi, může růst maximálně 3 roky, a tedy má maximálně 3 vrstvy. Můžeme to tedy brát tak, že nad každou větví v této vrstvě vyroste libovolná tříletka. Podobně jde spočítat počet tříletek pomocí počtu dvouletek, a tak dále. S pořádnou notací by to vypadalo následovně: Počet stromů s maximálně \(n\) vrstvami (tedy n-letky) nazveme \(S(n)\). Hledáme \(S(4)\). Stromů, které ještě nijak nevyrostly, tedy \(S(0)\), je 1. Jinak umíme spočítat počet až \((n+1)\)-vrstvých stromů \(S(n+1)\) pomocí případů 1. vrstvy tohoto stromu:
Neobsahuje nic (\(1\) případ).
Je jedna větev vedoucí doprava (\(S(n)\) případů).
Je jedna větev vedoucí doleva (\(S(n)\) případů).
Dvě větve na obě strany (\(S(n)^2\) případů).
Máme tedy \(S(n+1) = S(n)^2 + 2S(n) + 1\). Pak už jenom počítáme \[\begin{aligned} S(0) &= 1, \\ S(1) &= 1^2 + 2 \cdot 1 + 1 = 4, \\ S(2) &= 4^2 + 2 \cdot 4 + 1 = 25, \\ S(3) &= 25^2 + 2 \cdot 25 + 1 = 676,\\ S(4) &= 676^2 + 2 \cdot 676 + 1 = 458329. \\\end{aligned}\] Takže výsledkem je \(458329\).
15. Lukáš dělá vstávy vstáv!:
Lukáše se každé ráno pokouší vzbudit budík. Pokaždé, když zazvoní, tak je \(20\%\) šance, že Lukáš vstane. Jinak jej Lukáš plácne, a budík znovu zazvoní za \(10\) minut. Při plácnutí má Lukáš ovšem \(1\%\) šanci, že trefí homerun, a budík znovu zazvoní až za \(24\) hodin. Za kolik minut Lukáš průměrně vstane?
Řešení
Označme \(x\) hledanou průměrnou dobu za kterou Lukáš vstane od momentu, kdy mu právě poprvé zazvonil budík. Jistě je šance \(0.2\), že vstal okamžitě. S pravděpodobností \(0.8\) tedy spí dál. V takovém případě je šance \(0.01\), že trefí homerun. Tedy šance na homerun je \(0.8\cdot 0.01\). Zároveň je šance \(0.8\cdot 0.99\) že pouze plácne budík a netrefí homerun, tedy bude spát dalších \(10\) minut. Nejdůležitější úvaha je, že v případě, kdy bude spát do dalšího zvonění budíku (tedy například dalších 10 minut), bude v okamžiku dalšího zazvonění (po deseti minutách) průměrný čas za který od této doby vstane stejný, jako byl průměrný čas, za který vstane od prvního zvonění (jsme totiž nyní v úplně stejné situaci, pouze už uběhlo \(10\) minut). Z této úvahy sestavíme rovnici:
\[\begin{aligned} x=0.8\cdot 0.99\cdot (x+10)+0.8\cdot 0.01\cdot (x+24\cdot 60).\end{aligned}\] Vyřešením této lineární rovnice dostáváme odpověď \(x=97.2\).